Day01 Basic Mathematics Review (1)

📚 The Start of Recording TIL Summer ‘24 : Why Did I Start This Project? 🚀

🔔 Don't Miss: Continous Records of TIL '25 (Still On-Going!) 🌟

✨ A New Chapter in TIL '25: Reflecting, Growing, and Moving Forward 📖

Scalar, Norm, Matrix (Inverse, Basic Functions), Rank

One of my previous courses: Machine Learning Statistics Review

ML Stat Review

Scalar

• An element of a field which is used to define a vector space

Vector

• A mathematical object that has both a magnitude and direction

• Two vectors are the same, if they have - the same magnitude & direction - if they are the same, their cosine similarity is 1

Matrix

• A matrix is an array of numbers sized ‘m by n’. - m = #rows, n = #columns

Norm

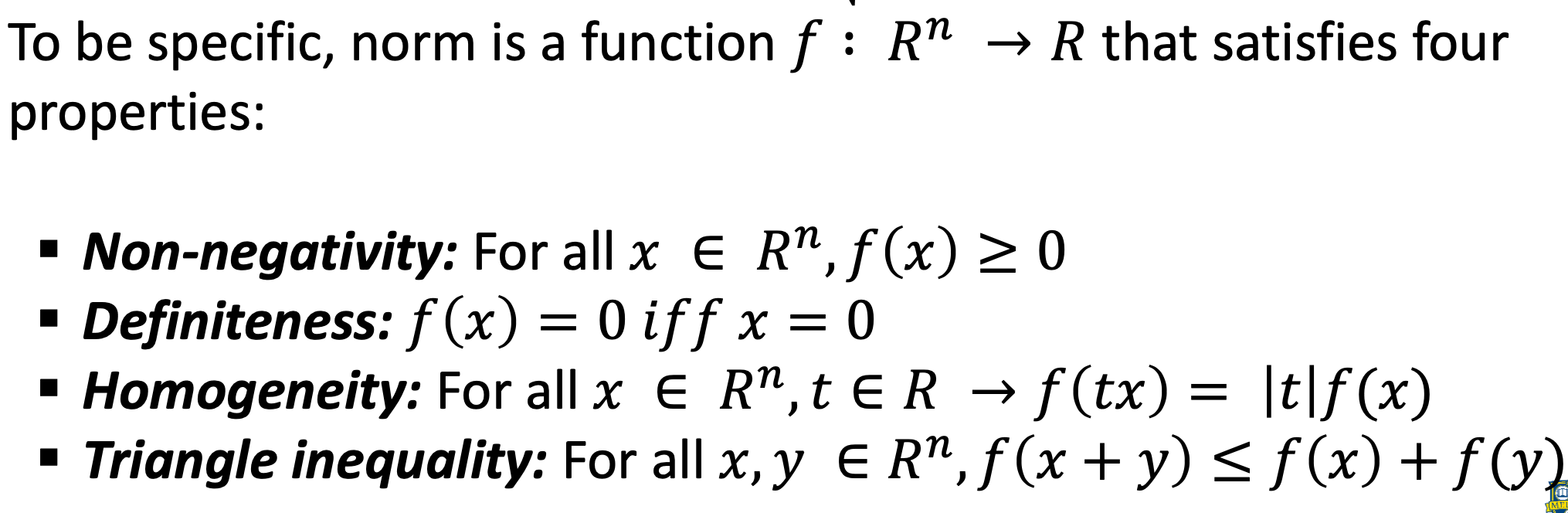
Matrix Operations

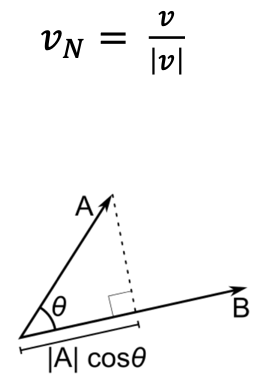
• Unit vector: a vector of length 1, also called normalized vector

• How do we convert a vector into a unit vector?

  
  

• Dot product (inner product) of vectors

  Multiply corresponding entries of two vectors and add up the result —> useful for a proxy for the angle between two vectors (Ex. If B is a unit vector, then A*B gives the length of A which lies in the direction of B)

• Product of two matrices

  matrix multiplication is associative & distributive & not commutative

• Transpose: A matrix flipped over its diagonal

  Useful for Rotation, Scaling, and Data Manipulation.

Determinant

• Can only be calculated for square matrices
• Useful: The area of an n-dimensional parallelogram is the determinant

Matrix Inverse

• When the determinant is zero, a matrix is not invertible.

• How useful?

  We can multiply a matrix by its inverse.

Pseudoinverse 유사역행렬 (Explained by Korean)

• If you want to use an inversed Matrix even though it is not a Square Matrix (Square Matrix가 아닌 경우에도 역행렬을 사용하고 싶을 경우)
• Generalized inverse or Moore-Penrose inverse (특이값 분해(Single Value Decomposition svd)를 이용하면 무어-펜로즈 유사 역행렬을 쉽게 계산할 수 있다)
• Use:
  • Compute a ‘best fit’ solution to a system of linear equations.
  • Find the minimum norm solution to a system of linear equations.
• Matrix is non-invertible: matrices are sparse( have many zero) / very large / very small.

Linear (in)dependence

• Linear independence: No vector is a linear combination of the other vectors
• Common cause: One of the vectors is a null vector , Or the vectors are perpendicular to each other

Matrix Rank

• The maximum number of linearly independent column vectors
• 𝐶𝑜𝑙 − 𝑟𝑎𝑛𝑘 𝐴 = 𝑅𝑜𝑤 − 𝑟𝑎𝑛𝑘(𝐴) (always!)
• Rank tells the dimension of an output (when you want to transform a matrix)
• If a square matrix (m x m) is rank m, we say it’s ’full rank.’
• If rank < m, we say it’s ‘singular.’
  • At least one dimension is a linear combination of another dimension
  • There is no inverse