Day10 ML Review - Gradient

📚 The Start of Recording TIL Summer ‘24 : Why Did I Start This Project? 🚀

🔔 Don't Miss: Continous Records of TIL '25 (Still On-Going!) 🌟

✨ A New Chapter in TIL '25: Reflecting, Growing, and Moving Forward 📖

Understanding Gradients in Machine Learning Applications

What is Gradient?

The term “gradient” in mathematics, particularly in calculus and vector calculus, is a vector that points in the direction of the greatest rate of increase of a scalar field. Its magnitude represents the rate of increase in that direction. This concept is fundamental in machine learning and optimization, where the gradient is crucial for finding the minimum or maximum of a function, typically used in optimizing loss functions.

Mathematical Definition

If you have a function $ f: \mathbb{R}^n \to \mathbb{R}$, which means $f$ is a function of multiple variables (for example, $f(x,y,z)$ in three-dimensional space), the gradient of $f$ at a point is a vector that consists of the partial derivatives of $f$ for each variable. It is denoted as $\nabla f$ or $grad\ f$.

For a function $f(x_1, x_2, \dots, x_n)$, the gradient is :

$\nabla f = (\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, ..., \frac{\partial f}{\partial x_n})$

From this, the vector represents the direction of the steepest slope, where the value of the function increases most rapidly. For example, if we have a function $f(x, y) = x^2 + y^2 + xy$, then the gradient is $\nabla f = (2x + y, 2y + x)$.

Starting from the point (1, 3), the direction in which the value of the function f increases most rapidly is (5, 7), and the slope, which represents the steepness of increase, is $ \rVert(5, 7) \lVert = \sqrt{5^2 + 7^2} = \sqrt{74}$.

Reference in Korean

다변수 함수 $f$ 가 $n$ 개 변수로 이루어져 있다면이 때 그래디언트(gradient)는 함수 $f$ 를 각 변수로 편미분(Partial derivative)한 값을 원소로 하는 벡터라고 정의할 수 있습니다. 이 벡터는 기울기가 가장 가파른 곳으로의 방향, $f$ 값이 가장 가파르게 증가하는 방향을 의미합니다. 예를 들어, $f(x, y) = x^2 + y^2 + xy$ 라고 하면, 그래디언트는 $\nabla f = (2x + y, 2y + x)$ 입니다. 임의의 점 (1,3) 에서 함수 $f$ 갑싱 최대로 증가하는 방향은 (5,7) 이고, 그 기울기 (벡터의 크기, 증가의 가파른 정도)는 $ \rVert(5, 7) \lVert = \sqrt{5^2 + 7^2} = \sqrt{74}$ 입니다.

• Properties of the Gradient

  • Direction: The gradient points in the direction of the steepest ascent in the function value. By the steepest ascent, we mean the direction in which the function increases most rapidly.

  • Magnitude: The magnitude of the gradient vector gives the rate of increase of the function at that point concerning the direction in which the function increases most rapidly.

• Applications in Machine Learning In machine learning, especially in training algorithms like gradient descent, the gradient is used to determine how to change the model parameters (like weights in neural networks) to minimize the loss function. The basic idea is:

  1. Calculate the gradient of the loss function with respect to the model parameters.
  2. Update the parameters in the direction opposite to the gradient because this direction decreases the function most rapidly (assuming minimization of the loss).

For example, if $L(\theta)$ is a loss function where $\theta$ represents model parameters, the gradient $\nabla_\theta L(\theta)$ tells us how $L$ changes with changes in $\theta$. To minimize $L$, we update $\theta$​ as follows:

$$ \theta_{\text{new}} = \theta_{\text{old}} - \alpha \nabla_\theta L(\theta_{\text{old}}) $$

where $\alpha$​ is the learning rate, a positive scalar that determines the step size of the update.

Gradient in Optimization

• Convex Functions: For convex functions, following the negative gradient guarantees that we will reach the global minimum.
• Non-convex Functions: For non-convex functions, following the negative gradient might lead to a local minimum, a saddle point, or a plateau, but not necessarily the global minimum.
  
  
  

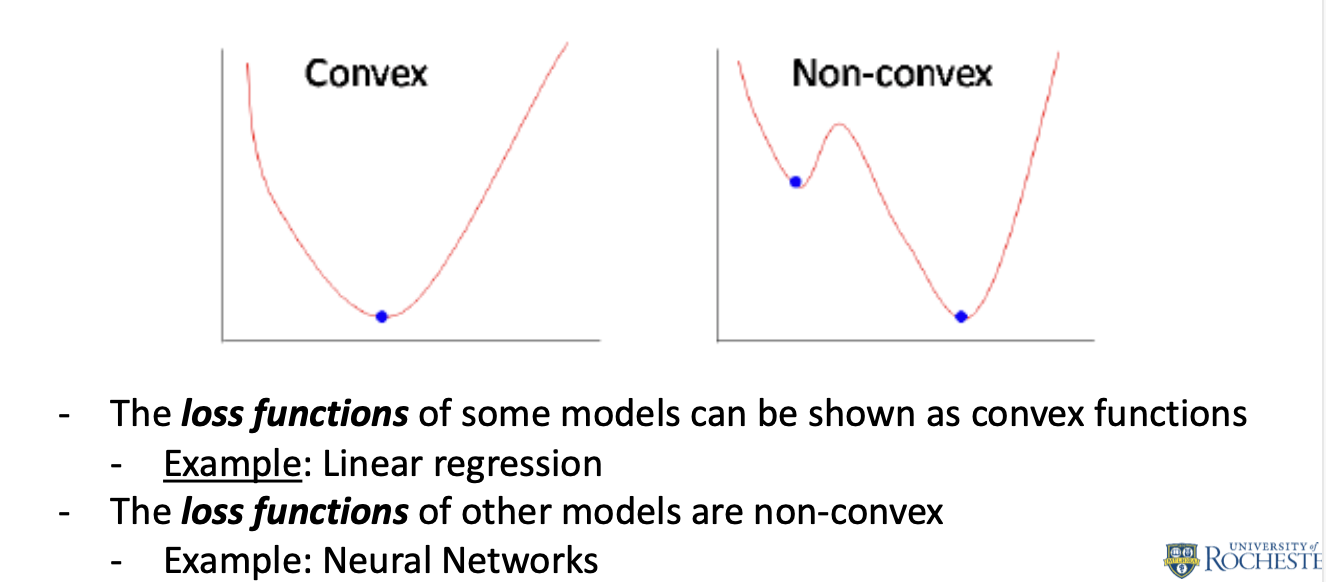
(DSCC465 Introduction to Statistical Machine Learning, Prof. Cantay Caliskan, University of Rochester, Spring 2024)