Day02 Basic Mathematics Review (2)
Norm(2), Eigenvectors and Eigenvalues

Type of Norm
The L1 Norm & L2 Norm are both ways to measure the size or length of a vector, and they are frequently used in various contexts with mathematics, computer science, and machine learning.
-
L1 Norm
- The L1 norm of a vector (Manhattan Norm)
- The Sum of Absolute Value
- It can be visualized as the distance you would travel between two points in a grid-like path (like navigating city blocks), which accounts for its alternative name, the “Manhattan distance.”
-
L2 Norm
- The L2 norm (Euclidean Norm)
- The Sum of Squares of the vector’s element
- Represents the straight-line distance from the origin to the point in Euclidean space described by the vector. It corresponds to the length of the hypotenuse of a right-angled triangle, extending this concept to n-dimensional space.
Later, we will discuss the application of these norms further. FYI, in machine learning and computer science, the choice between L1 and L2 norms often depends on the application’s specific requirements, such as the need for robustness against outliers, preference for sparsity, or the mathematical properties required by the optimization algorithm.
Eigenvector and eigenvalue
Eigenvectors and eigenvalues are fundamental concepts in linear algebra that have extensive applications across various fields, including physics, engineering, and machine learning, particularly in methods like Principal Component Analysis (PCA) and spectral clustering.
-
An eigenvalue is a scalar associated with a linear transformation represented by a matrix. It quantifies the factor by which the magnitude of an eigenvector is scaled during the transformation.
For a given square matrix 𝐴, a scalar 𝜆 is an eigenvalue if there exists a non-zero vector 𝑣 such that: 𝐴𝑣 = 𝜆𝑣. Applying the matrix 𝐴 to the vector 𝑣 results in a new vector that is a scalar multiple of 𝑣, where 𝜆 is the scalar.
-
An eigenvector v is a non-zero vector of a linear transformation A that does not change its direction when this linear transformation A is applied to it.
-
That is, after a linear transformation, eigenvectors are vectors that remain parallel (do not change their direction) by an $n \times n$ square matrix $A$, and eigenvalues represent the degree of change in length.
-
Geometrically, the eigenvectors of the matrix (linear transformation) $A$ represent direction vectors whose direction is preserved and only scale is changed by the linear transformation $A$, and the eigenvalues represent the degree of scale change of those eigenvectors.
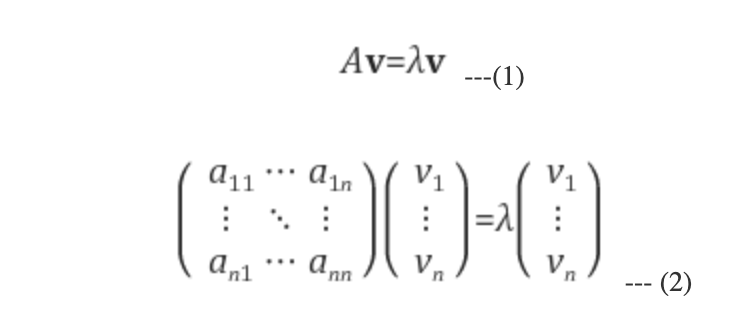
- Application and Importance
- PCA (Principal Component Analysis): Eigenvectors are used to determine the directions of maximum variance in high-dimensional data, with the corresponding eigenvalues indicating the magnitude of these variances. This method is fundamental in reducing dimensions while retaining as much variability as possible.
Reference in Korean
$Ax = \lambda x$ 식에서 $\lambda$는 고유값eigenvalues, $x$는 고유벡터eigenvectors를 각각 나타내며, $n \times n$ 정방행렬 $A$에 의해 선형 변환Linear Transformation 을 시켜도 변환 전과 후가 평행한parallel 벡터를 고유벡터eigenvectors, 그리고 길이 변화량의 정도를 나타낸 것을 고유값이라 한다.
A행렬에서 곱해질 때, 거의 모든 벡터들은 방향을 바꾼다. 특정한 예외적인 벡터 $x$는 $Ax$와 동일한 방향이다. 그러한 벡터들을 고유벡터eigenvectors라고 한다. $A$ 를 고유벡터eigenvectors에 곱하고, 그렇게 곱해진 벡터 $Ax$는 기존의 $x$에 $\lambda$를 곱한 것이 된다.
기하학적으로 봤을 때, 행렬(선형 변환) A의 고유벡터는 선형변환 A에 의해 방향Direction 은 보존되고 스케일만 변화되는 방향벡터를 나타내고, 고유값은 그 고유벡터의 변화되는 스케일scale 정도를 나타내는 값이다.

Leave a comment