Day21 Probability Review (3)
Continuous Probability Distribution and Markov Chains

(Ace the Data Science Interview: 201 Real Interview Questions Asked By FAANG, Tech Startups, & Wall Street)
Probability Distribution
Different probability distributions can be applied to specific situations. For instance, we can calculate the probability of a specific event occurring by using the distribution’s probability density function (PDF).
2. Continous Probability Distributions
The uniform distribution assumes a constant probability of a value falling between the intervals $a$ to $b$. Its PDF is
Mean: $\mu = \frac{a+b}{2}$
Variance: $\sigma^2 = \frac{(b-a)^2}{12}$
The most common applications for a uniform distribution are in sampling (random number generation, for example) and hypothesis testing cases.
The exponential distribution provides the probability of the time between events occurring in a Poisson process with a given rate parameter $\lambda$. It’s PDF is
Mean: $\mu = \frac{1}{\lambda}$
Variance: $\sigma^2 = \frac{1}{\lambda^2}$
The exponential distribution is commonly used for wait times, such as the time between customer purchases or credit defaults. One of its most useful properties is “memorylessness,” which gives rise to natural questions about the distribution.
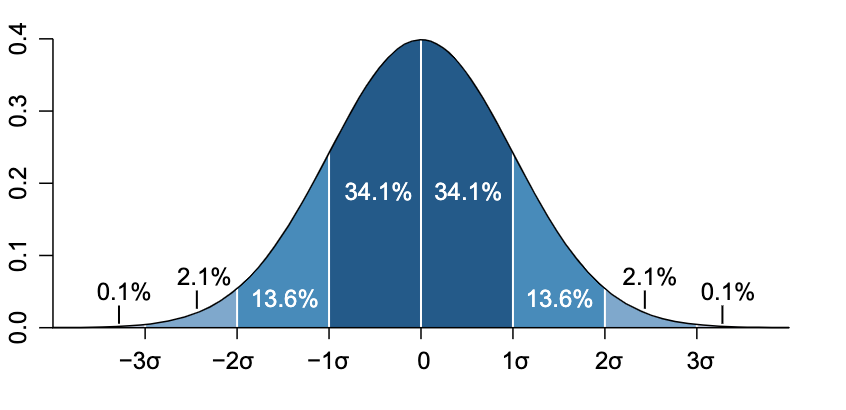
The normal distribution is a probability distribution that follows the well-known bell curve pattern over a specific range. Given a particular mean and variance, its PDf is:
Mean: $\mu = \mu$
Variance: $\sigma^2 = \sigma^2$
 (Image:https://en.wikipedia.org/wiki/Probability_distribution)
(Image:https://en.wikipedia.org/wiki/Probability_distribution)
Many real-life applications frequently rely on the normal distribution due to its natural fit and the Central Limit Theorem (CLT). Thus, it is crucial to remember the probability density function (PDF) of the normal distribution.
Markov Chains
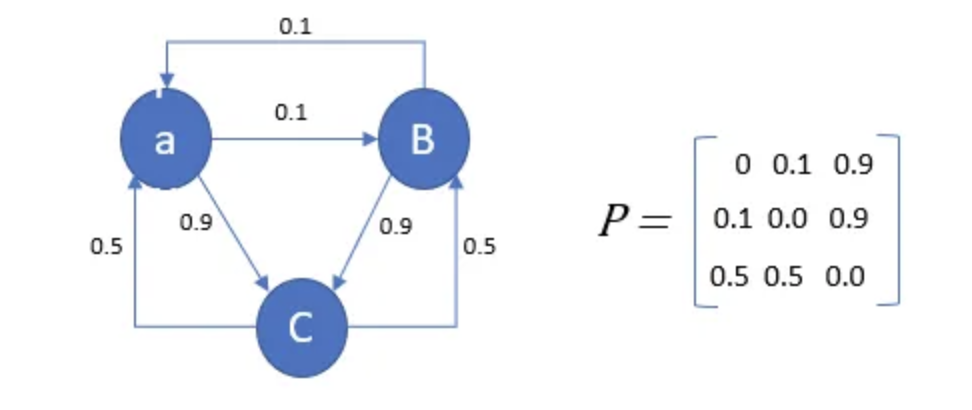
A Markov chain is a process in which there is a finite set of states, and the probability of being in a particular state only depends on the previous state.
(https://builtin.com/machine-learning/markov-chain)
A Markov chain is a stochastic model created by Andrey Markov that describes the probability of a sequence of events occurring based on the state of the previous event. It is a widely used and easily understandable model frequently employed in industries dealing with sequential data, such as finance. Even Google’s page rank algorithm, which determines the priority of links in its search engine results, is a type of Markov chain. Utilizing mathematical principles, this model leverages observations to forecast future events.
The primary objective of the Markov process is to determine the probability of moving from one state to another. A key attraction of the Markov process is that the future state of a stochastic variable depends solely on its present state. The stochastic variable is informally defined as a variable whose values are based on the results of random events.
The term “memorylessness” in mathematics refers to a property of probability distributions where the time it takes for an event to occur does not depend on how much time has already passed. In a Markov process, predictions are conditional on their current state and independent of past and future states.
The Markov process has its benefits when predicting words or sentences based on previously entered text. The downside is that you won’t be able to predict text based on context from a previous state of the model, a common problem in natural language processing (NLP).
(https://towardsdatascience.com/markov-chain-analysis-and-simulation-using-python-4507cee0b06e)
(https://www.geeksforgeeks.org/markov-chains-in-nlp/)
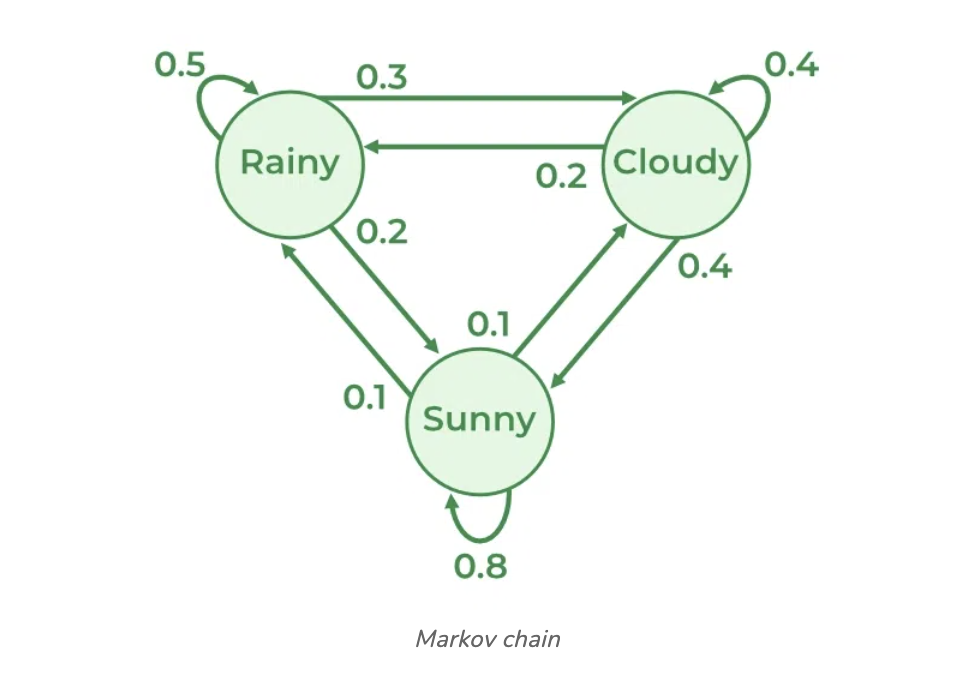
For instance, in natural language processing (NLP), we utilize the Markov chain as described earlier. When creating a sequence of weather states, we begin with an initial state and utilize the transition probabilities to randomly choose the next state. This process is repeated to generate a sequence of weather states.
Leave a comment