Day33 ML Review - Support Vector Machine (2)

📚 The Start of Recording TIL Summer ‘24 : Why Did I Start This Project? 🚀

🔔 Don't Miss: Continous Records of TIL '25 (Still On-Going!) 🌟

✨ A New Chapter in TIL '25: Reflecting, Growing, and Moving Forward 📖

SVM: Nonlinear Separable Case

(Python Machine Learning: Machine Learning and Deep Learning with Python, scikit-learn, and TensorFlow 2, 3rd Edition)

Slack variables, denoted as $\xi_i$, are introduced to allow some flexibility in positioning the data points relative to the margin. This leads to the so-called soft-margin classification for nonlinearly separable data to allow optimization convergence with appropriate cost penalization.

• For each training example $\mathbf{x}_i, y_i$, the slack variable $\xi_i$ quantifies the degree of misclassification or how far a data point is from meeting the margin requirements.

Modified Constraints

The constraints for the soft margin SVM are modified to incorporate slack variables:

$y_i (\mathbf{w}^T \mathbf{x}_i + b) \geq 1 - \xi_i$

where $ \xi_i \geq 0$ for all $i$.

• If $\xi_i = 0$, the point $\mathbf{x}_i$ is correctly classified and lies outside or on the margin.
• If $0 < \xi_i \leq 1$, the point $ \mathbf{x}_i $ is correctly classified but lies inside the margin.
• If $\xi_i > 1$, the point $\mathbf{x}_i$ is misclassified.

So, the new objective to be minimized, subject to the constraints, becomes:

$$ \frac{1}{2} \Vert W \Vert^2 + C(\sum_i \xi^{(i)}) $$

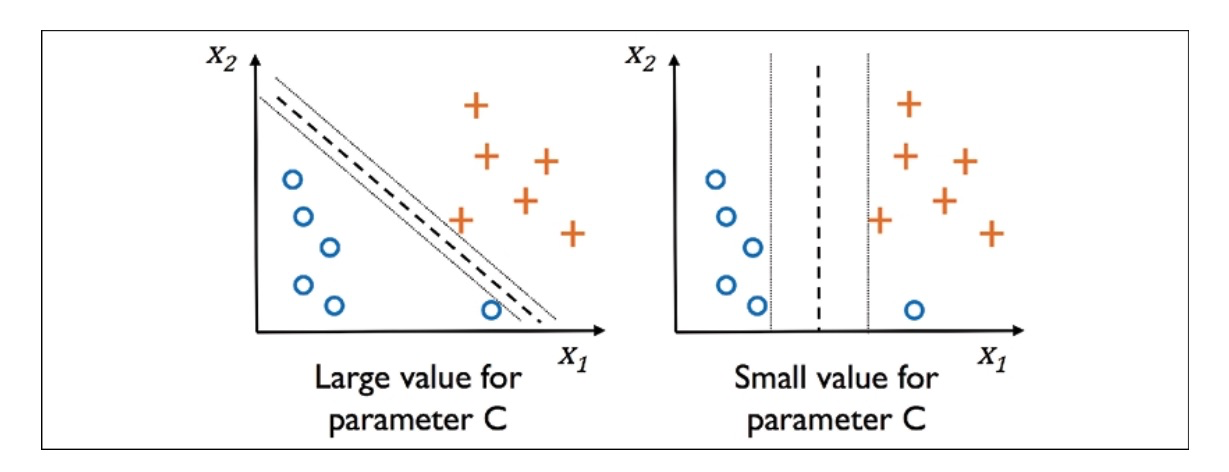
By adjusting variable C, we can control the penalty for misclassification. Choosing larger values for C leads to larger error penalties, while smaller values make us less strict about misclassification errors. It is related to regularization, in which decreasing the value of C increases the bias and lowers the variance of the model.

(Python Machine Learning: Machine Learning and Deep Learning with Python, scikit-learn, and TensorFlow 2, 3rd Edition)

Cost Function

The objective function is also modified to penalize the slack variables, balancing the margin maximization and the classification error:

$\min_{\mathbf{w}, b, \xi} \frac{1}{2} \|\mathbf{w}\|^2 + C \sum_{i=1}^{m} \xi_i $

where $C$ is a regularization parameter that controls the trade-off between maximizing the margin and minimizing the classification error.

Side Notes (SVM vs LR)

In practical classification tasks, linear logistic regression and linear SVMs often produce very similar results. However, there are key differences in their approaches and sensitivities. Logistic regression aims to maximize the conditional likelihoods of the training data, making it more vulnerable to outliers. Conversely, SVMs concentrate on the data points closest to the decision boundary, known as support vectors, which reduces their sensitivity to outliers.

Logistic regression is also advantageous because of its simplicity and ease of implementation. Another significant benefit is that logistic regression models can be easily updated, making them well-suited for applications involving streaming data.