Day56 ML Review - Cross Validation (1)
Model Selection and K-Fold Cross Validation
When constructing a machine learning model, evaluating its performance based on data on which it has yet to be trained is essential. For example, if we train our model using a particular dataset, we need to assess its performance when presented with new data that it has yet to see.
As we’ve discussed, a model can suffer from underfitting (high bias) if it’s too simple or overfitting the training data (high variance) if it’s too complex. The key is to evaluate our model meticulously to strike an acceptable balance between bias and variance.
We will check holdout cross-validation and k-fold cross-validation, which can help us obtain reliable estimates of the model’s generalization performance, such as how well the model performs on unseen data.
The Holdout Method
Estimating the generalization performance of machine learning models often involves using the holdout cross-validation approach, a classic and popular method. This technique includes splitting the initial dataset into separate training and test datasets. The training dataset is then used to train the model, while the test dataset assesses its generalization performance.
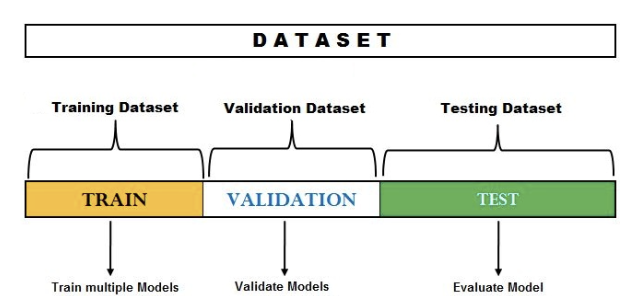
(Image from: https://vitalflux.com/hold-out-method-for-training-machine-learning-model/)
In typical machine learning scenarios, it’s crucial to fine-tune and compare different parameter configurations to enhance predictive performance on new data. This process, known as model selection, involves identifying the best tuning parameters (hyperparameters) for a specific classification problem. However, reusing the same test dataset multiple times during model selection can lead to it becoming part of our training data, increasing the risk of overfitting. Despite this challenge, many practitioners still utilize the test dataset for model selection, considered poor machine learning practice.
A more effective approach to employing the holdout method for model selection involves dividing the data into three distinct parts: a training dataset, a validation dataset, and a test dataset. (1) The training dataset is utilized to train various models, and (2) the validation dataset is then employed to select the best model based on performance. The diagram below depicts the concept of holdout cross-validation, where a validation dataset is used to assess the model's performance after training with various hyperparameter values.
(3)Once the hyperparameter values are appropriately fine-tuned, the model's overall performance is evaluated using the test dataset.
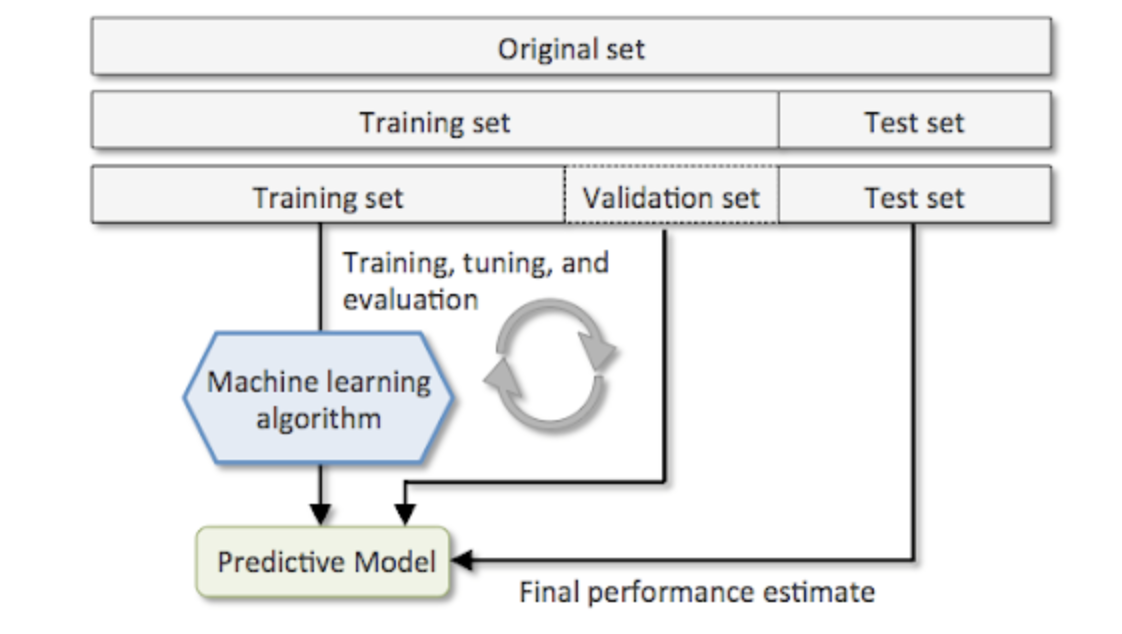
(Image from: https://vitalflux.com/hold-out-method-for-training-machine-learning-model/)
K-Fold Cross-Validation
Using the holdout method, we can estimate the performance of a model by repeating it $k$ times on $k$ subsets of the training data.
In $k$-fold cross-validation, the training dataset is randomly split into $k$ folds without replacement. Out of these folds, $k-1$ is used for model training, and the remaining $1$ fold is used for performance evaluation. This process is repeated k times to create $k$ models and performance estimates.
To obtain a performance estimate that is less sensitive to the training data's sub-partitioning than the holdout method, we calculate the average performance of the models based on different independent test folds. We typically use k-fold cross-validation for model tuning, which involves finding the optimal hyperparameter values that result in satisfactory generalization performance. This is estimated by evaluating the model performance on the test folds.
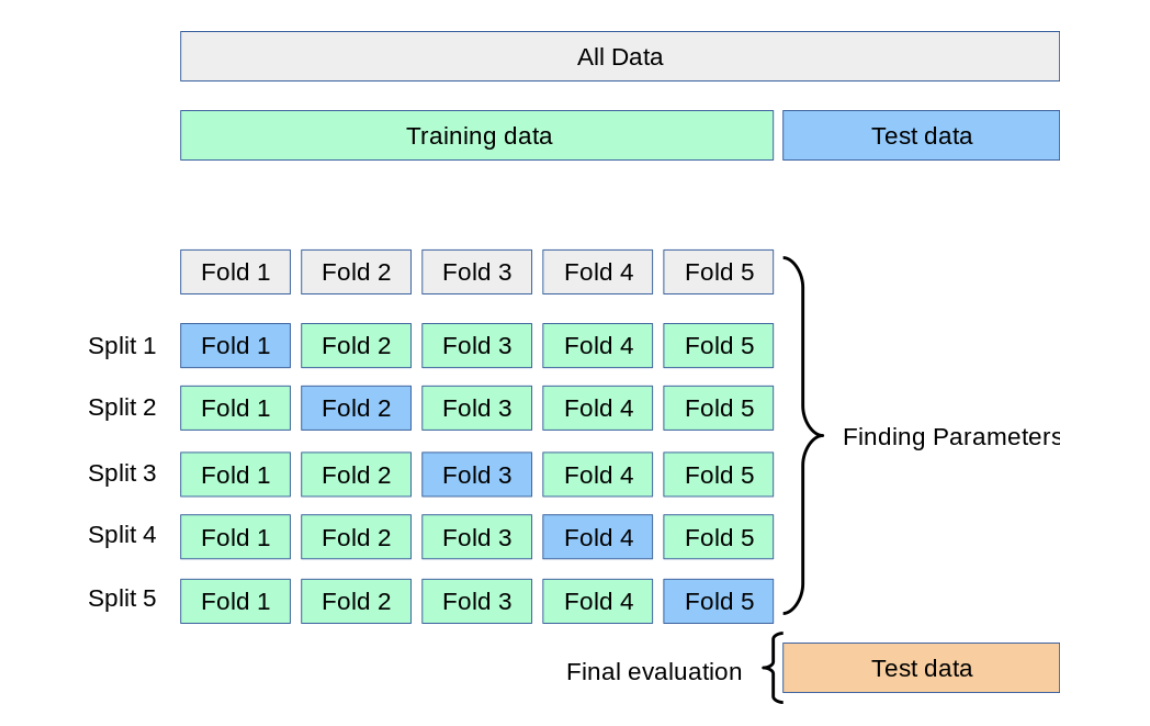
After finding suitable hyperparameter values, we can retrain the model using the entire training dataset. This allows us to obtain a final performance estimate using the independent test dataset. Fitting the model to the whole training dataset after k-fold cross-validation is necessary because providing more training examples to a learning algorithm generally leads to a more accurate and reliable model.
K-fold cross-validation is a resampling technique that does not replace data. This method ensures that each example is used for training and validation exactly once, as part of a test fold. As a result, it yields a more stable estimate of the model’s performance compared to the holdout method.
When working with a small training set, increasing the number of folds in cross-validation is beneficial to reduce bias. However, using large values of $k$ will increase runtime and result in higher variance estimates. For larger datasets, a smaller value of $k$ can still accurately estimate the model’s average performance, reducing computational costs.
A stratified k-fold cross-validation approach is a refined version of the standard k-fold cross-validation method. This approach is beneficial when dealing with imbalanced class proportions as it can provide more accurate bias and variance estimates.
Below is creating a stratified K-Fold cross-validation algorithm from scratch.
import numpy as np
from sklearn.model_selection import StratifiedK-Fold
kfold = StratifiedKFold(n_splits=10).split(X_train, y_train)
scores = []
for k, (train, test) in enumerate(kfold):
pipe_lr.fit(X_train[train], y_train[train])
score = pipe_lr.score(X_train[test], y_train[test])
scores.append(score)
print('Fold: %2d, Class dist.: %s, Acc: %.3f' % (k+1, np.bincount(y_train[train]), score))
We initialized the StratifiedKFold iterator in the code, passing in the y_train class labels from the training dataset and specifying the number of folds using the n_splitsparameter. We ensured that the examples were appropriately scaled throughout each iteration, such as standardizing them using the pipe_lr pipeline. Subsequently, we used the test indices to compute the accuracy score of the model, gathering the scores in a list to calculate the average accuracy and the standard deviation of the estimate later.
We can use scikit-learn's k-fold cross-validation scorer, which allows for evaluating our model using stratified k-fold cross-validation more concisely, as below.
from sklearn.model_selection import cross_val_score
scores = cross_val_score(estimator=pipe_lr,
X=X_train,
Y=y_trian,
cv=10,
n_jobs=1)
print('CV accuracy scores: %s' % scores)
print('CV accuracy: %.3f +/- %.3f' % (np.mean(scores), np.std(scores)))
Leave a comment