Day62 ML Review - Ensemble Method (1)

📚 The Start of Recording TIL Summer ‘24 : Why Did I Start This Project? 🚀

🔔 Don't Miss: Continous Records of TIL '25 (Still On-Going!) 🌟

✨ A New Chapter in TIL '25: Reflecting, Growing, and Moving Forward 📖

Key Concepts and Mathematics Explanation

Key Concepts

Ensemble methods aim to combine different classifiers into a meta-classifier, which can provide better generalization performance than each classifier alone.

For example, assuming that we collected predictions from 10 experts, ensemble methods would allow us to strategically combine those predictions by the ten experts to come up with a more accurate and robust prediction than each expert’s predictions.

Ensemble methods frequently utilize the majority voting principle, where the class label that is predicted by the majority of classifiers is selected, signifying that it has received over 50 percent of the votes. This approach can be expanded to handle multiclass scenarios through plurality voting, in which the class label that garners the highest number of votes (the mode) is chosen.

Ensembles can be constructed using various classification algorithms. For instance, decision trees, support vector machines, logistic regression classifiers, and others can be used depending on the technique. Alternatively, the same base classification algorithm can be employed to fit different subsets of the training dataset. A well-known example of this approach is the random forest algorithm, which combines multiple decision tree classifiers.

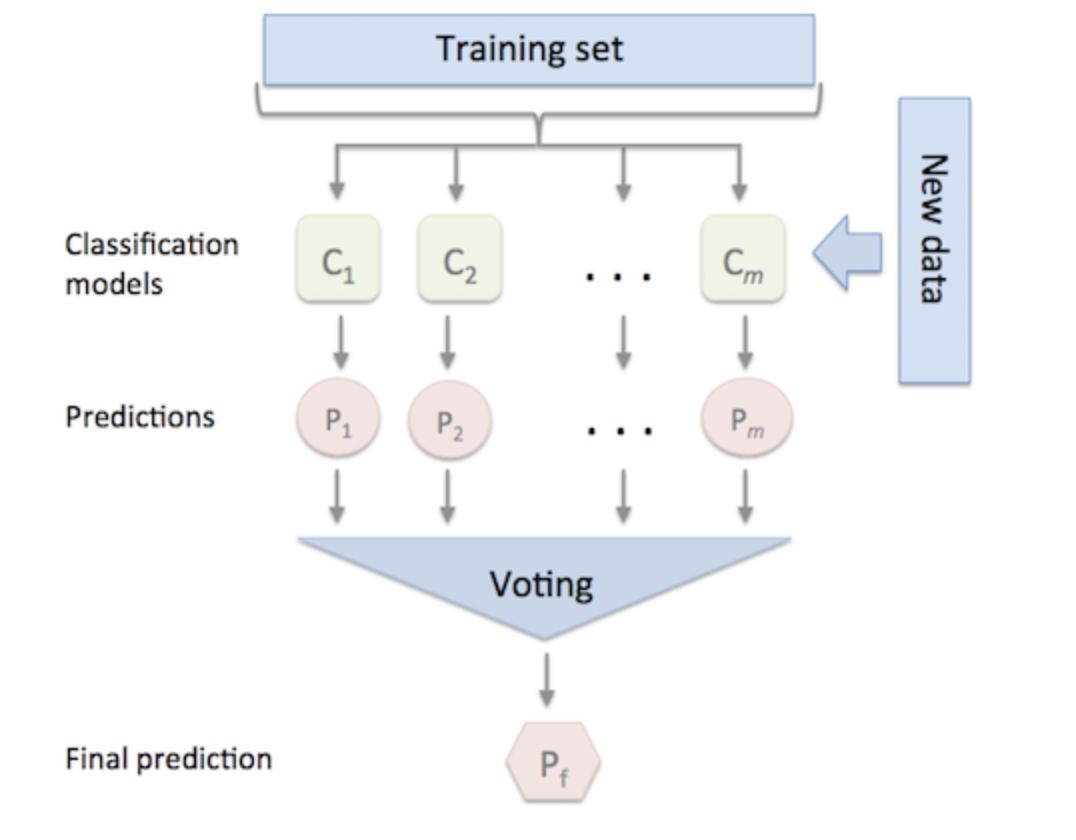
Image from (https://rasbt.github.io/mlxtend/user_guide/classifier/EnsembleVoteClassifier/)

The EnsembleVoteClassifier implements “hard” and “soft” voting. In hard voting, we predict the final class label as the class label predicted most frequently by the classification models. In soft voting, we predict the class labels by averaging the class probabilities (only recommended if the classifiers are well-calibrated).

Mathematics

To predict a class label through simple majority or plurality voting, we combine the predicted class labels of each classifier, $C_j$, and select the class label, $\hat{y}$, with the most votes.

$\hat{y} = \text{mode} \{ C_1(x), C_2(x), \dots , C_m(x) \} $

For example, in a binary classification task where class1 = -1 and class2 = +1, we can write the majority vote prediction as follows.

$$ C(x) = \text{sign} \left( \sum_{j=1}^{m} C_j(x) \right) = \begin{cases} 1 & \text{if } \sum_{j=1}^{m} C_j(x) \geq 0 \\ -1 & \text{otherwise} \end{cases} $$

To understand why ensemble methods can outperform individual classifiers, let’s use basic combinatorics. Consider this example: we assume that all $n$-base classifiers for a binary classification task have the same error rate ($\epsilon$). Furthermore, we assume that the classifiers are independent and their error rates are uncorrelated. Under these assumptions, we can express the error probability of an ensemble of base classifiers as a probability mass function of a binomial distribution.

$$ P(y \geq k) = \sum_{k}^{n} \binom{n}{k} \epsilon^k (1-\epsilon)^{n-k} = \epsilon_{ensemble} $$

Here, $\binom{n}{k}$ is the binomial coefficient $n$ choose $k$. In other words, we compute the probability that the prediction of the ensemble is wrong. Now, let’s take a look at a more concrete example of 11 base classifiers ($n = 11$), where each classifier has an error rate of 0.25 ($\epsilon = 0.25$):

$$ P(Y \geq k) = \sum_{k=6}^{11} \binom{11}{k} \epsilon^k (1-\epsilon)^{11-k} = 0.034 $$

As observed here, the ensemble’s error rate (0.034) is much lower than each classifier’s error rate (0.25) if all assumptions are met. We can also compare this using Python code.

>>> from scipy.special import comb
>>> import math
>>> def ensemble_error(n_classifier, error):
  k_start = int(math.ceil(n_classifier / 2.))
  probs = [comb(n_classifier, k) * error**k *
          (1-error)**(n_classifier-k)
          for k in range(k_start, n_classifier+1)]
  			return sum(probs)
>>> ensemble_error(n_classifier=11, error=0.25)
0.03432750701904297

We will use matplotlib to observe by implementing the resulting plot.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> error_range = np.arrange(0.0, 1.01, 0.01)
>>> ens_errors = [ensemble_error(n_classifier=11, error=error)
                 for error in error_range]
>>> plt.plot(error_range, ens_errors, label="Ensemble Error", linewidth=2)
>>> plt.plot(error_range, error_range, linestyle='--', label='Base Error', linewidth=2)
>>> plt.xlabel('Base Error')
>>> plt.ylabel('Base/Ensemble Error')
>>> plt.legend(loc='upper left')
>>> plt.grid(alpha=0.5)
>>> plt.show()

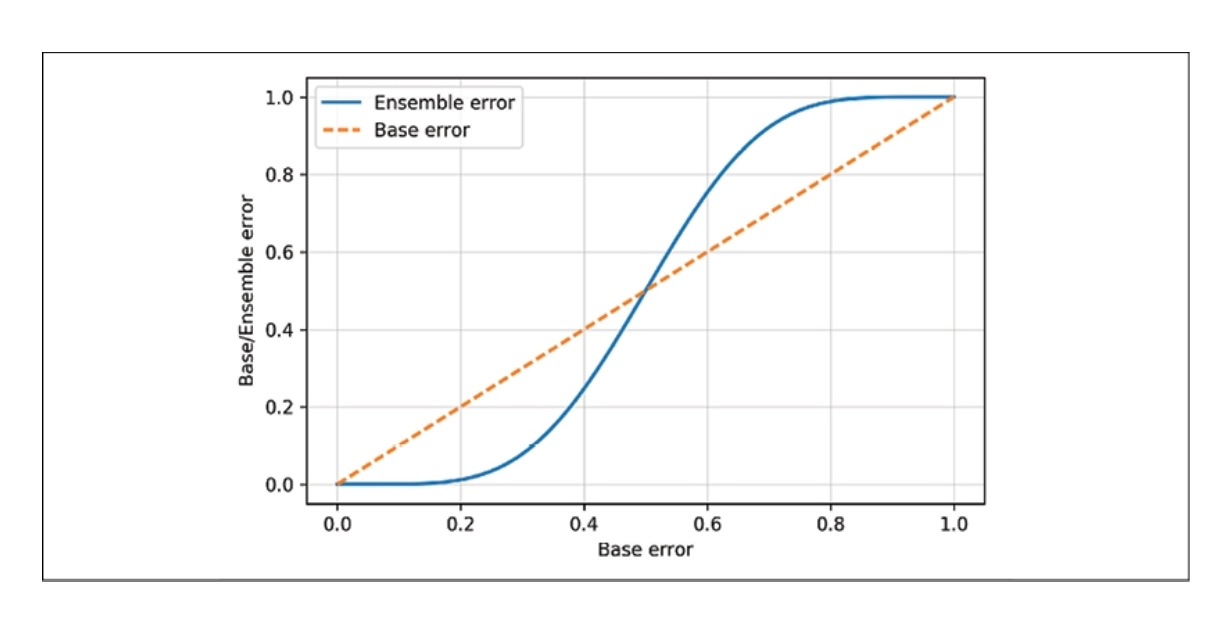
As we can see in the resulting plot below, the error probability of an ensemble is always better than the error of an individual base classifier as long as the base classifiers perform better than random guessing ($\epsilon$< 0.5).