Day67 Deep Learning Lecture Review - Lecture 2-3

📚 The Start of Recording TIL Summer ‘24 : Why Did I Start This Project? 🚀

🔔 Don't Miss: Continous Records of TIL '25 (Still On-Going!) 🌟

✨ A New Chapter in TIL '25: Reflecting, Growing, and Moving Forward 📖

Types of Learning and Neural Net Zoo: Fully Connected Networks (MLPs), Inductive Bias, and Convolutional Neural Networks (CNNs)

Paradigms Beyond Supervised Learning

Types of Learning

• Supervised Learning
  • Training data includes desired output.
  • classification & regression
• Unsupervised Learning
  • Training data does not include the desired output.
  • clustering, dimensionality reduction, density estimation
• Self-Supervised Learning
  • Training data labels itself somehow.
• Reinforced Learning
  • A type of machine learning where an agent learns to behave in an environment by performing actions and seeing the results, often as rewards or punishments
  • In supervised learning, a function approximation such as ‘f(x)=y’ is given to the model, but in RL, within the environment, the agent can take actions at each time step, and it is not told exactly what to do.
  • The model gets a scaler reward signal.
    • ex) Won the game $\rightarrow$ +1, or lost the game -1
  • Wants to maximize the reward
  • Examples
    • Gaming:
      • AlphaGo: The program developed by DeepMind that learns to play the board game Go and can compete against top human players.
      • Video Game Play: Agents developed to play and master complex video games like those from the Atari game suite.
    • Robotics:
      • Autonomous Vehicles: Developing driving policies for autonomous cars that can navigate complex traffic scenarios.
      • Robotic Manipulation: Robots learning to manipulate objects through trial and error, improving their ability to perform tasks such as assembly-line work or surgical operations.

Neural Net Zoo

We will reivew a high-level neural network architectures, which are all based on the MLP. The goal is to get to know deeper with the Inputs and Outputs of each of the number of nerural network systems.

Fully Connected Networks (MLPs)

• MLP is a class of fully connected feedforward neural networks. It consists of input layers, one or more hidden layers, and an output layer. Every node (neuron) in one layer is connected to every node in the next layer, hence the term “fully connected.”

• Critical Characteristics of MLP:
  • General Purpose: MLPs are applicable to a range of tasks, including classification and regression. However, they do not naturally leverage data structures like images or time series.
  • Fixed Input Size: MLPs require fixed-size input data (flattened into a vector), which means they don’t naturally handle high-dimensional data like images without preprocessing.
  • Lack of Spatial Awareness: MLPs do not consider the spatial structure of the data, making them less efficient for tasks like image recognition, where local relationships between pixels are essential.
• MLPs have been extended to handle other forms of data.

  • It is often used in other networks.

  • Sequential inputs and sets (text, audio, etc.): RNNs (many types), Transformers (many types)
  • Graphs: Graph neural networks (many types)
  • Images and Video: Convolutional Neural Network, Vision Transformers
  • Every type of neural network architecture features layers with specific characteristics.
    • You can combine them freely.
• Ofthen MLP layers are used near the top of many network architectures to facilitate classification / regression

Inductive Bias

• Inductive Bias: Assumptions built into the learning algorithm.
  • It refers to the set of assumptions a learning algorithm makes to generalize from a limited set of training data to unseen instances. These biases help guide the learning process, influencing how the model interprets data and makes predictions.

• Inductive biases are essential because, in most cases, the training data does not fully capture every possible variation in the data, and without some assumptions, a model would have difficulty generalizing beyond the specific examples it has seen.

• Aspects of Inductive Bias
  • Assumptions about the Data: Inductive bias assumes certain properties about the underlying data, such as smoothness, continuity, or simplicity of relationships, which allows the model to generalize effectively. For example, a linear regression model assumes that the relationship between features and the target is linear.
  • Constraining the Hypothesis Space: Inductive bias narrows down the set of possible solutions (hypotheses) that a learning algorithm can choose from. For instance, in neural networks, inductive bias is introduced by the architecture (e.g., convolutional layers in CNNs assume local spatial correlations in image data).
  • Prior Knowledge: The inductive bias of a model may incorporate prior knowledge or assumptions about the domain, such as specific symmetries, hierarchical structures, or domain-specific constraints. For example, in Graph Neural Networks (GNNs), the assumption is that information can be propagated and aggregated between connected nodes in a graph.
  • Trade-off: The right amount of inductive bias can lead to better generalization, while too little bias may lead to overfitting (memorizing training data), and too much bias may lead to underfitting (over-simplifying the relationships in the data).

​

• Examples of Inductive Bias in Algorithms
  • Linear regression: Assumes a linear relationship between input features and the output.
  • Decision trees: Assume that a hierarchical structure of binary decisions is appropriate for classification.
  • Convolutional Neural Networks (CNNs): Assume spatial locality (nearby pixels are related) and translational invariance (features are the same regardless of position).

Convolutional Neural Networks (CNNs)

• Definition
  • A form of neural network that has an inductive bias
    • Use convolutional units (spatially tied weights) implemented via linear filtering
• A deep learning neural network architecture that learns directly from data. CNNs are particularly useful for finding patterns in images for object, class, and category recognition.
• Convolutional Neural Network (CNN) is a specialized type of deep neural network designed for processing data that has a grid-like structure, such as images or time-series data.

Components of CNN

(source: IBM: What is CNN?)

• Convolutional Layers: The core building block of CNNs is the convolutional layer, which uses small filters (or kernels) to slide over the input data and perform a mathematical operation called convolution. Each filter detects specific patterns like edges, textures, or shapes from local regions of the input. The output of this operation is a feature map, which highlights the presence of certain features in the input.
• Receptive Field: Each neuron in a convolutional layer only looks at a small region (the “receptive field”) of the input, which allows the CNN to capture local features. As we move deeper into the network, the layers can combine these local features to capture more abstract and complex patterns.
• Weight Sharing: Unlike fully connected layers, where every connection has its own weight, CNNs use the same filter across different regions of the input. This weight sharing makes CNNs much more efficient in terms of the number of parameters, especially when processing large inputs like images.
• Pooling Layers: After the convolution operation, CNNs often use pooling layers (e.g., max pooling or average pooling) to reduce the spatial dimensions of the feature maps. Pooling helps to downsample the data, making the network less sensitive to small translations and reducing the computational complexity.
• Activation Functions: Following each convolutional layer, CNNs typically use an activation function like ReLU (Rectified Linear Unit) to introduce non-linearity, allowing the network to learn more complex patterns and relationships within the data.
• Fully Connected Layers: Toward the end of the network, after several convolutional and pooling layers, CNNs often use one or more fully connected (dense) layers. These layers process the high-level features extracted by the convolutional layers to make predictions, such as classifying an image.

• Output Layer: The output layer typically uses a softmax function for classification tasks, where the network outputs a probability distribution over the possible classes.

• Fully Connected MLP network vs. Convolutional Neural Network

  
  Perceptron
  (Image from: Simplilearn - Multilayer Perceptron)
  
  
  
  
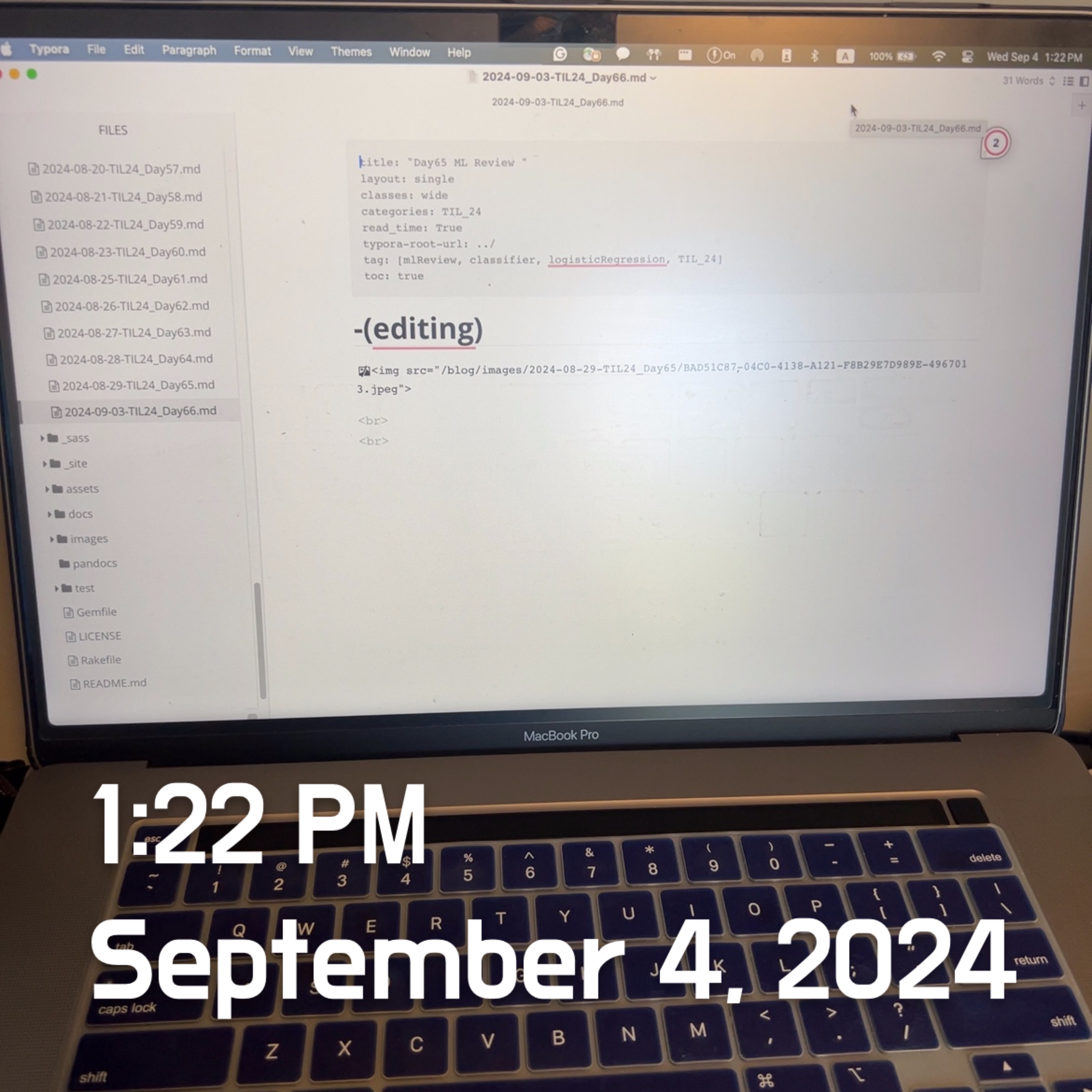
  • Perceptron
    • Perceptron rule and Adaline rule were used to train a single-layer neural network
    • Weights are updated based on a unit function in perceptron rule or on a linear function in Adaline Rule.
  
  Multi-Layered ANN
  (Image from: Simplilearn - Multilayer Perceptron)
  
  
  
  

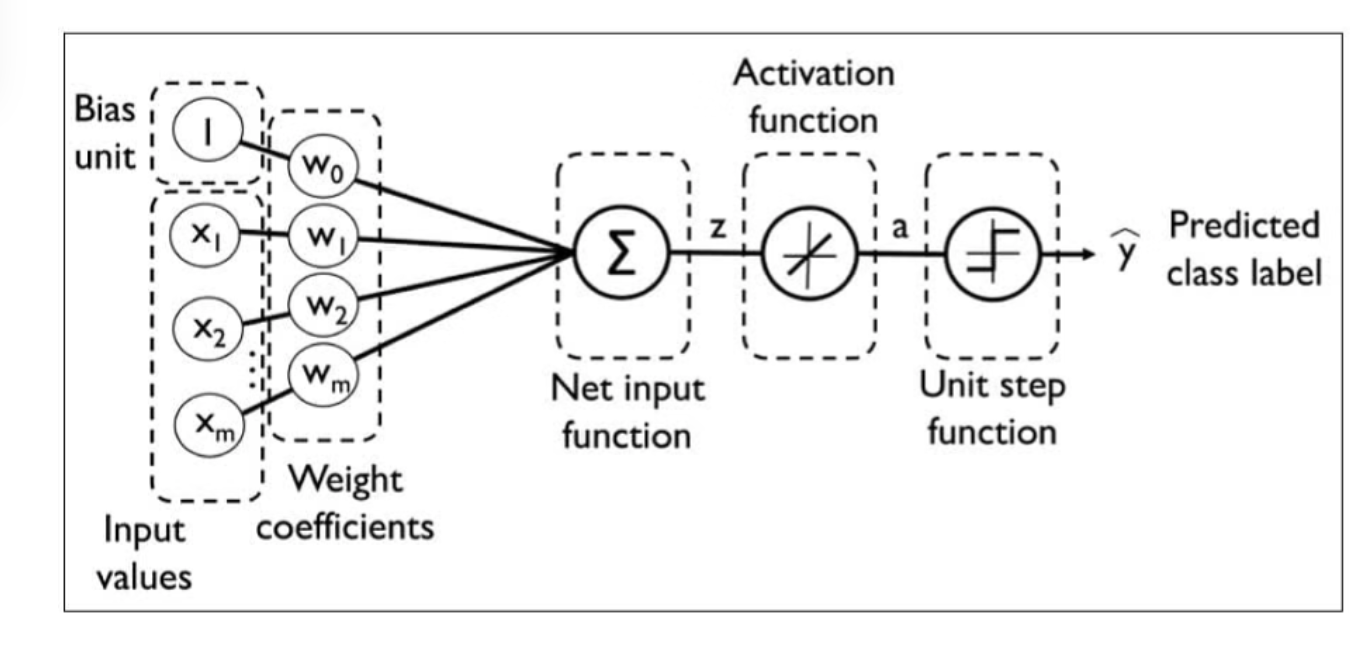
  • Multi-Layer Perceptron

    • A fully connected multi-layer neural network is called a Multilayer Perceptron (MLP).

    • It has 3 layers including one hidden layer. If it has more than 1 hidden layer, it is called a deep ANN. An MLP is a typical example of a feedforward artificial neural network.

    • To optimize a neural network, it’s important to adjust the number of layers and neurons, which are referred to as hyperparameters. This process involves using cross-validation techniques to identify the most effective values for these parameters.

    • Weight adjustment training in neural networks involves backpropagation, a process in which the network adjusts the weights of its connections to reduce errors. Deeper neural networks can encounter vanishing gradient problems, where the gradient becomes extremely small, hindering the learning process.

      Feature	MLP (Fully Connected)	CNN (Convolutional Neural Network)
      Basic Unit	Neuron	Convolutional Unit
      Unit Input	Vector	Tensor (3D for images: width, height, channels)
      Unit Output	1 number (scalar)	Feature Map (tensor)

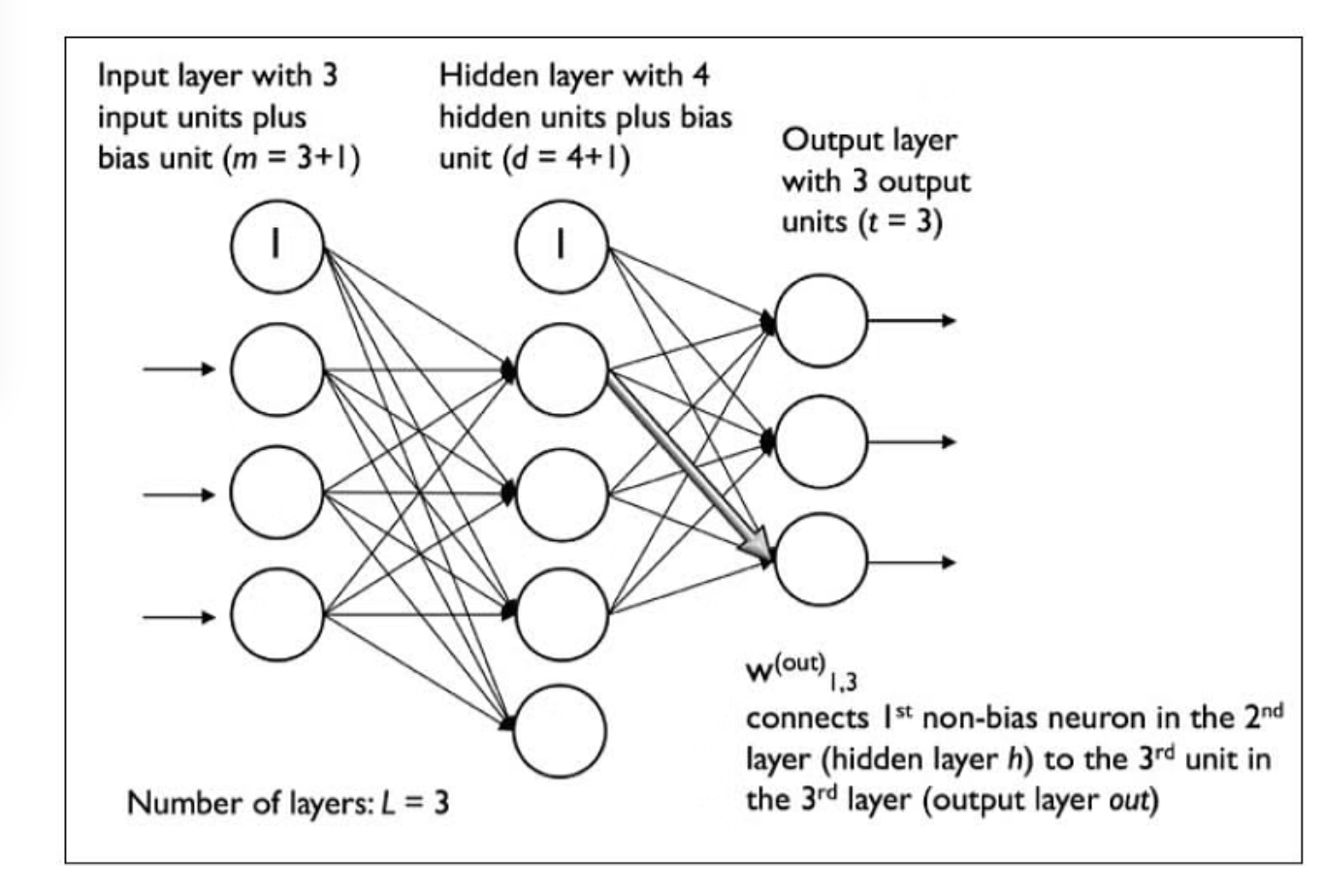
• How does Convolutional Network work?
  

  
  
  
  

  CNNs process data hierarchically. In early layers, they capture low-level features like edges, corners, and textures. As you go deeper into the network, the layers start to combine these features into more complex structures, like shapes, objects, and eventually, entire scenes. This hierarchical learning enables CNNs to perform exceptionally well on image-related tasks.

• Convolutional Units are Linear filters

  • CNN learn filters in each laer
  • A CNN unit takes as input a tensor and produces a feature map (i.e.., a matrix or a slice of the output tensor)

• 2D Linear Filters
  • A 2D linear filter takes as input a tensor and outputs a feature map
  • A 2d linear filter has a spatial dimension.
  • The input needs to be padded to make sure the output has the same spatial dimensions

• Convolutional Layer mathematics

  $h_i^n = max \big\{ 0, \sum_{j=1}^{\#input \ channels}h_j^{n-1} * w_{ij}^n \big\}$
  
  

  When $h_i^n$ is output feature map, $h_i^{n-1}$ is input feature map, and $w_{ij}^n$ is kernel.