Day69 DL Review - Convolutional Neural Networks (CNNs)
Basic Concepts and the Detailed Architecture

Basic Concepts of CNNs
Explanation from: Medium: Understanding CNN
CNN, which stands for Convolutional Neural Networks, is mainly used for processing image or video data in deep learning. As the name suggests, it is a neural network model that involves a preprocessing operation called convolution.
The reason for using CNN starts with the limitations of general DNN (Deep Neural Network). General DNN primarily uses one-dimensional data. When an image (for example, in a two-dimensional format such as 1028x1028) is used as an input, it must be flattened into single-line data. However, this flattening process causes the loss of spatial or topological information of the image. Additionally, due to the absence of an abstraction process, general DNN leads to poor learning time and efficiency.
CNN was created as a solution to these problems. It processes images as raw input and constructs a hierarchy of features while maintaining spatial/regional information. The key aspect of CNN is (1) analyzing parts of the image rather than the whole and (2) preserving the correlation between one pixel and its surrounding pixels in the image.
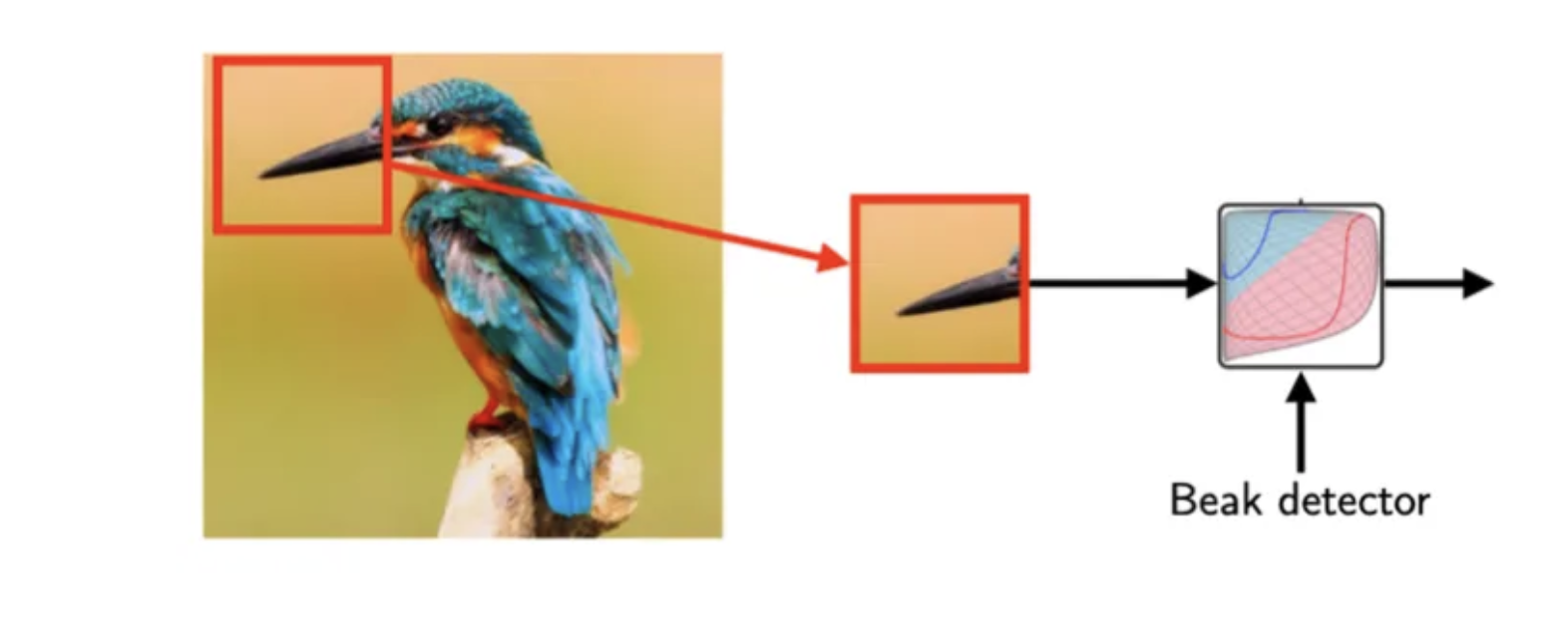
When we want to teach a computer to recognize whether a picture has a bird in it or not, we need to pay special attention to things like a bird’s beak. Even though the beak is just a small part of the whole bird, it’s really important for the computer to be able to figure out if it’s there. Instead of looking at the whole picture, a special kind of computer program called a Convolutional Neural Network, or CNN can look for specific patterns, like a bird's beak, without having to process the entire image.
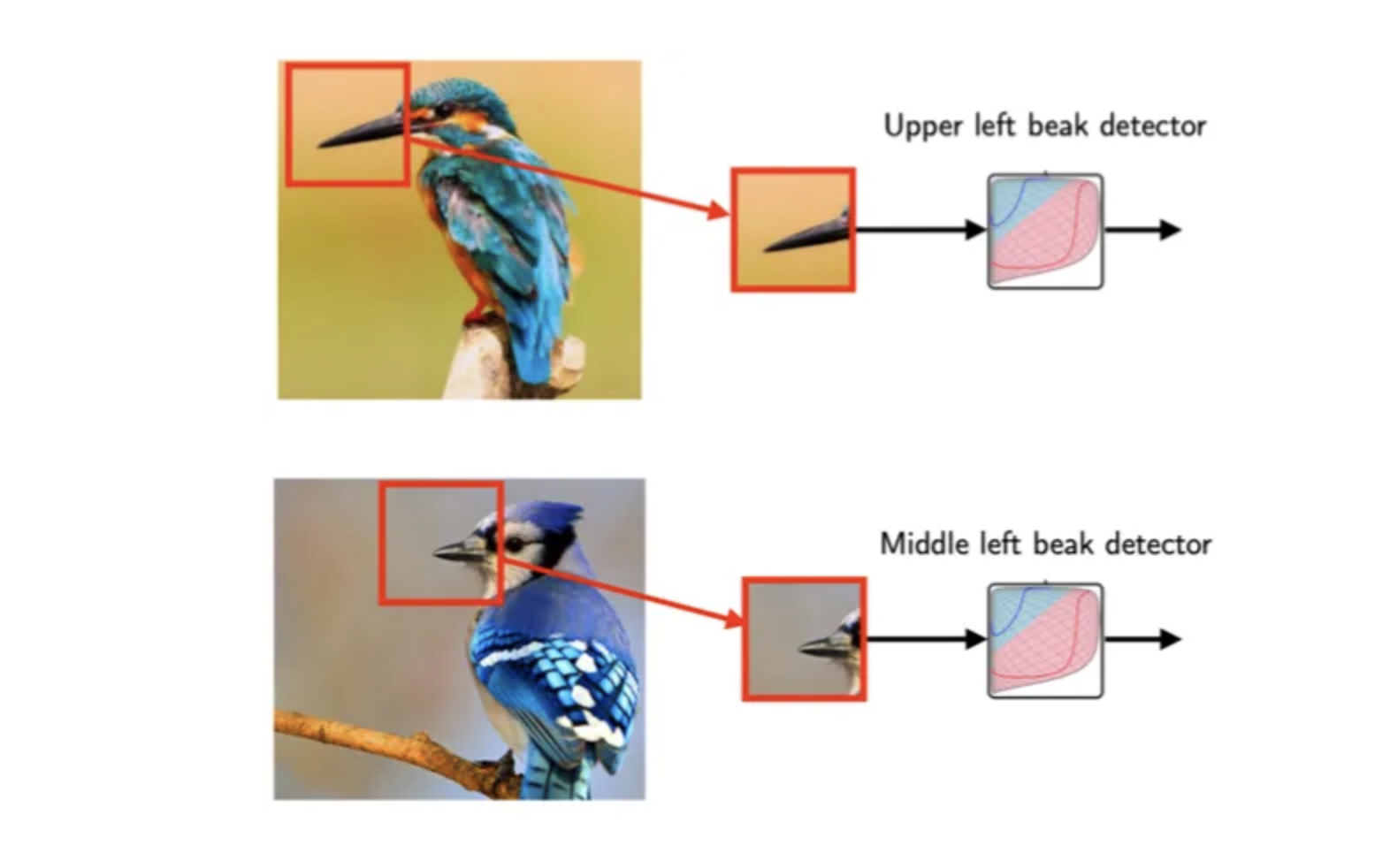
If you look at the two images above, you can see that the bird's beak is positioned differently. In the first image, the bird’s beak is located at the top left, while in the second image, it is situated slightly to the left of the top center. Therefore, it can be valuable and efficient to capture specific parts of the image rather than the entire image.
Understanding CNNs and Feature Hierarchies
A Convolutional Neural Network (CNN) analyzes an input image by breaking it down into smaller sections of pixels and then computing feature maps based on these local patches.
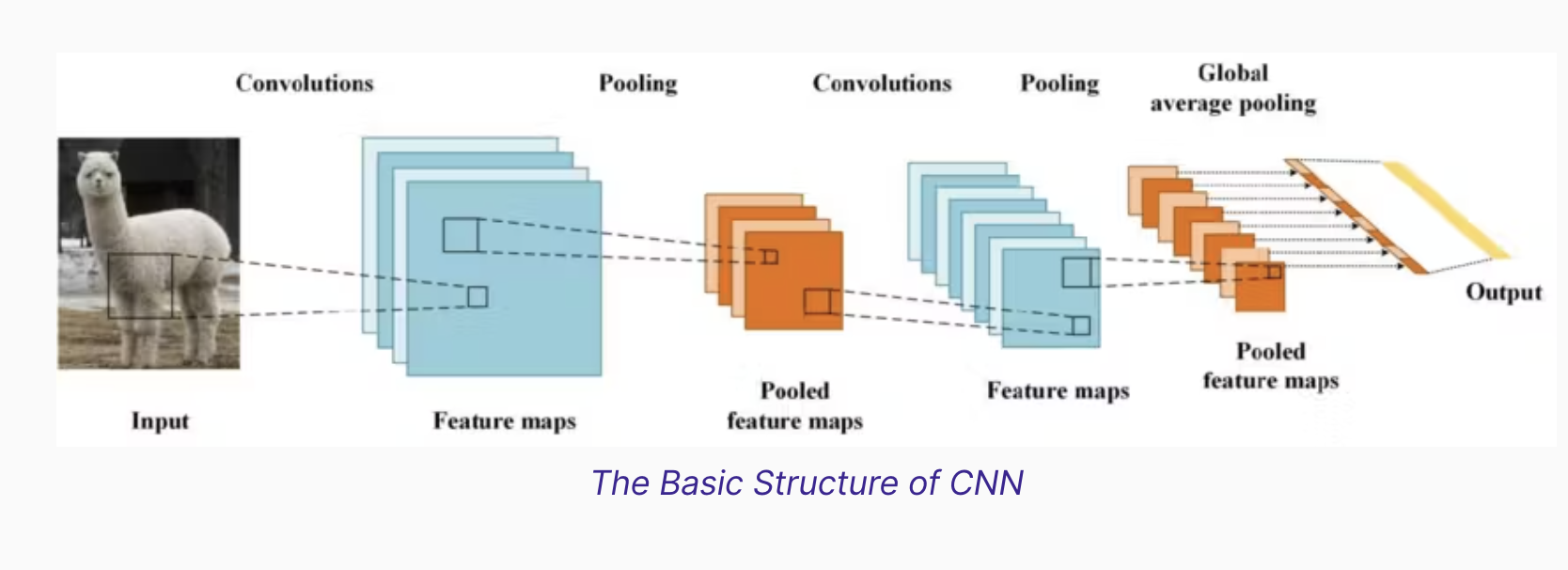
(https://encord.com/blog/convolutional-neural-networks-explained/)
When we switch from a traditional, fully connected Multilayer Perceptron (MLP) to a convolutional layer, a significant reduction in the network's weight (parameter) count is observed. This modification improves the network’s capacity to capture crucial features in the data. In the context of image data, it is reasonable to assume that nearby pixels are more relevant to each other than pixels that are far apart.
Convolutional Neural Networks (CNNs) are structured with multiple layers of convolutional and subsampling operations, followed by one or more fully connected layers at the end. The fully connected layers essentially form a Multi-Layer Perceptron (MLP), where each input unit, $i$, is connected to every output unit, $j$, using a weight denoted as $W_{ij}$.
The subsampling layers, also known as pooling layers, do not have any learnable parameters. This means they do not have adjustable weights or bias units during training. In contrast, both the convolutional and fully connected layers have weights and biases that are modified and optimized as the network is trained.
The Architecture of CNNs
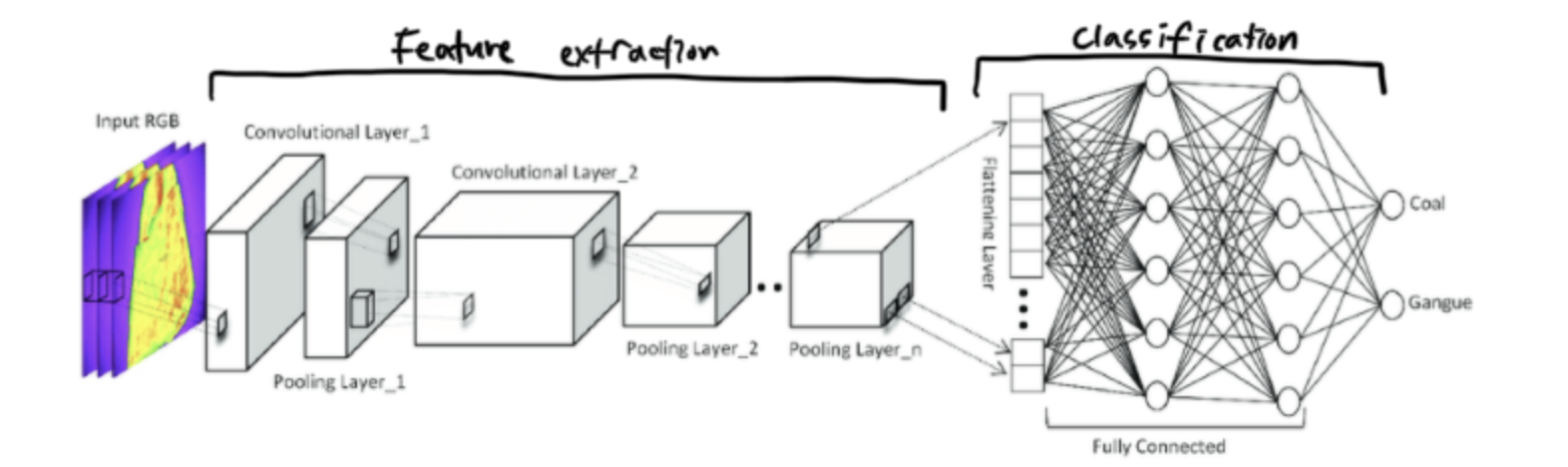
The architecture of a Convolutional Neural Network (CNN) is designed to take advantage of the 2D structure of an input image. This is achieved through convolutional layers, pooling layers, and fully connected layers. Each type of layer performs a distinct function and contributes to the network’s ability to perform complex image recognition tasks.
Image and explanations from Rubber-Tree blog
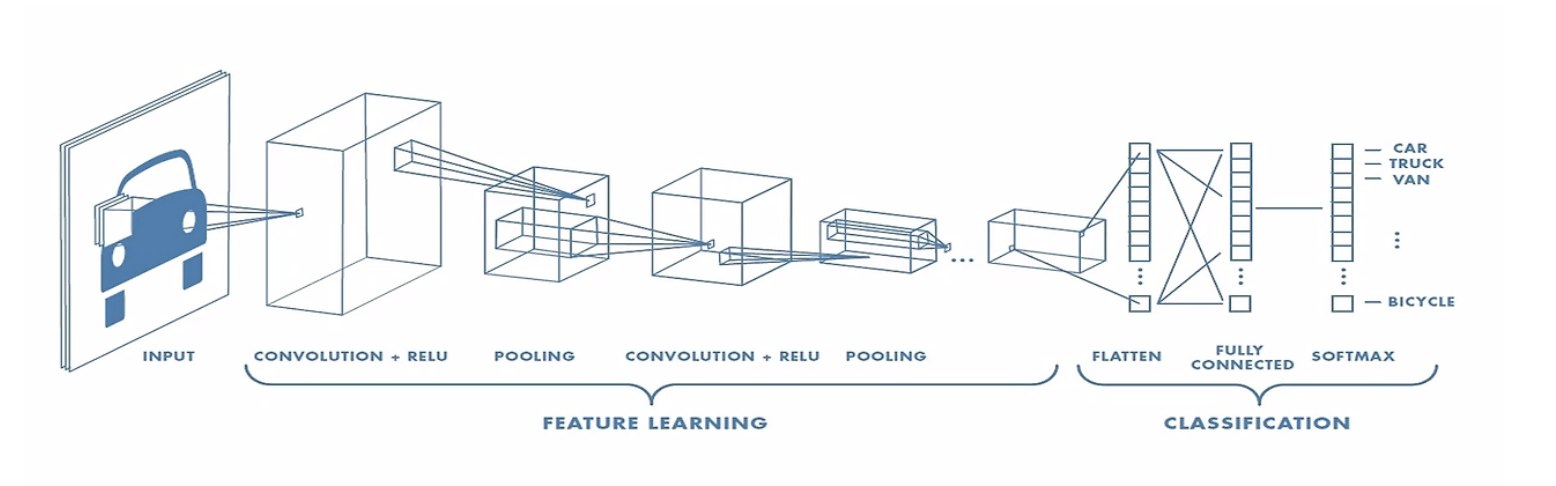
Convolutional Neural Networks (CNNs) are adept at leveraging the layered structure of an image to identify and extract features. They accomplish this by employing Convolution Layers, which apply different filters to the input image to identify and extract features, and Pooling Layers, which significantly reduce the data’s dimensionality. For classification purposes, CNNs make use of the Fully Connected Layer. Following feature extraction, the image is flattened before being fed into the Fully Connected Layer to finalize the classification process.
Convolution Layers
Color image data is typically represented as a three-dimensional tensor (3D tensor), allowing for encapsulation of the width, height, and channel dimensions. For instance, the color channels of an image in the RGB format consist of Red (R), Green (G), and Blue (B).
Filter Application
The application of filters is a fundamental technique in image processing, particularly in the context of Convolutional Neural Networks (CNNs). In a single convolution layer, there are as many filters as the number of channels in the input image. The output image of the convolution layer is created by applying the filter assigned to each channel.
How Filters Work:
A Convolutional Neural Network (CNN) analyzes an input image by breaking it down into smaller sections of pixels and then computing feature maps based on these local patches.
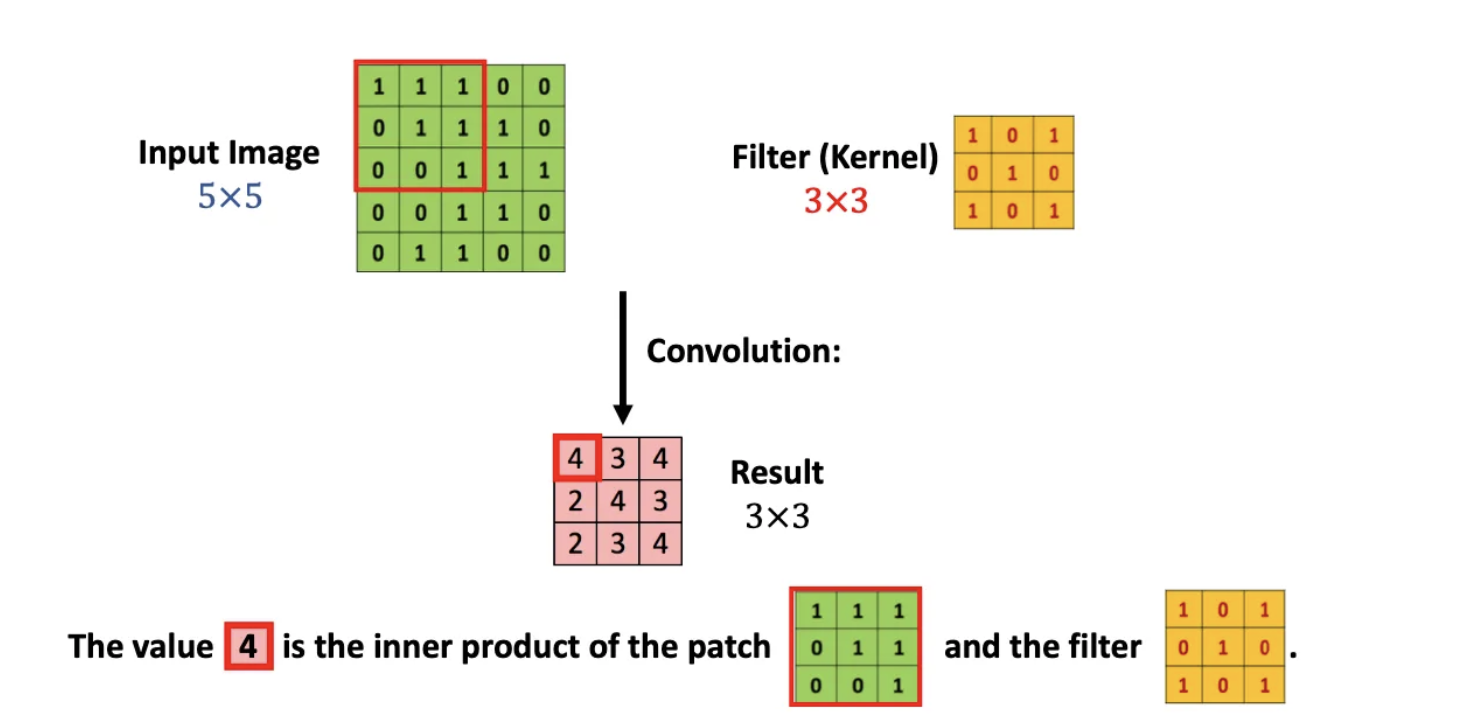
Let’s consider a more straightforward example where an image input is represented as a 5x5 matrix. We also have a 3x3 filter for our Convolutional Neural Network (CNN). Essentially, this single filter scans the entire image input to find and process patterns. We aim to apply the same filter to all input image areas repetitively. When we apply this filter to the image, it performs a calculation using the Inner Product between matrices.
Convolution Process: A filter (also known as a kernel) slides over the image, and at each position, it performs element-wise multiplication with the part of the image it covers. The results of these multiplications are then summed up to produce a single output pixel in the feature map. This operation is repeated across the entire image.
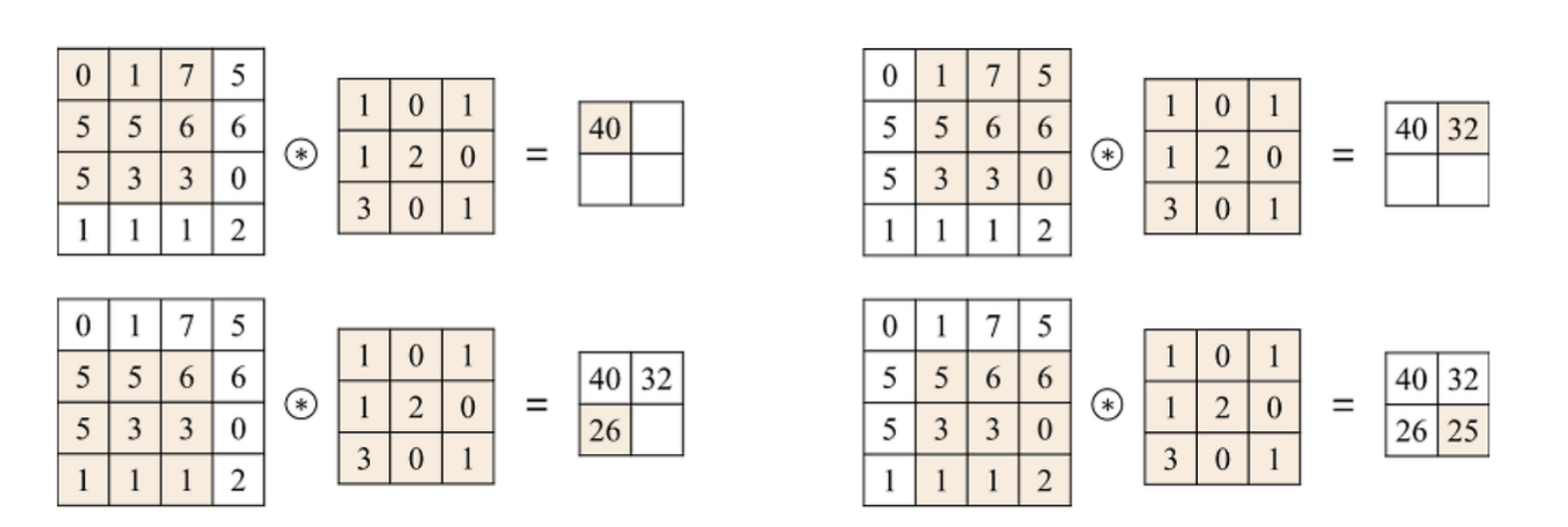
The example above applies a 3x3 filter to a 4x4x1 image segment, resulting in a 2x2x1 tensor image.
There are instances where the input is three-dimensional. For instance, a color image comprises three channels: R, G, and B, making its size three-dimensional, represented as $d_1 \times d_2 \times 3$. This shape is referred to as an order-3 tensor. Similarly, the standard two-dimensional image is also known as an order-2 tensor, which is essentially a matrix.
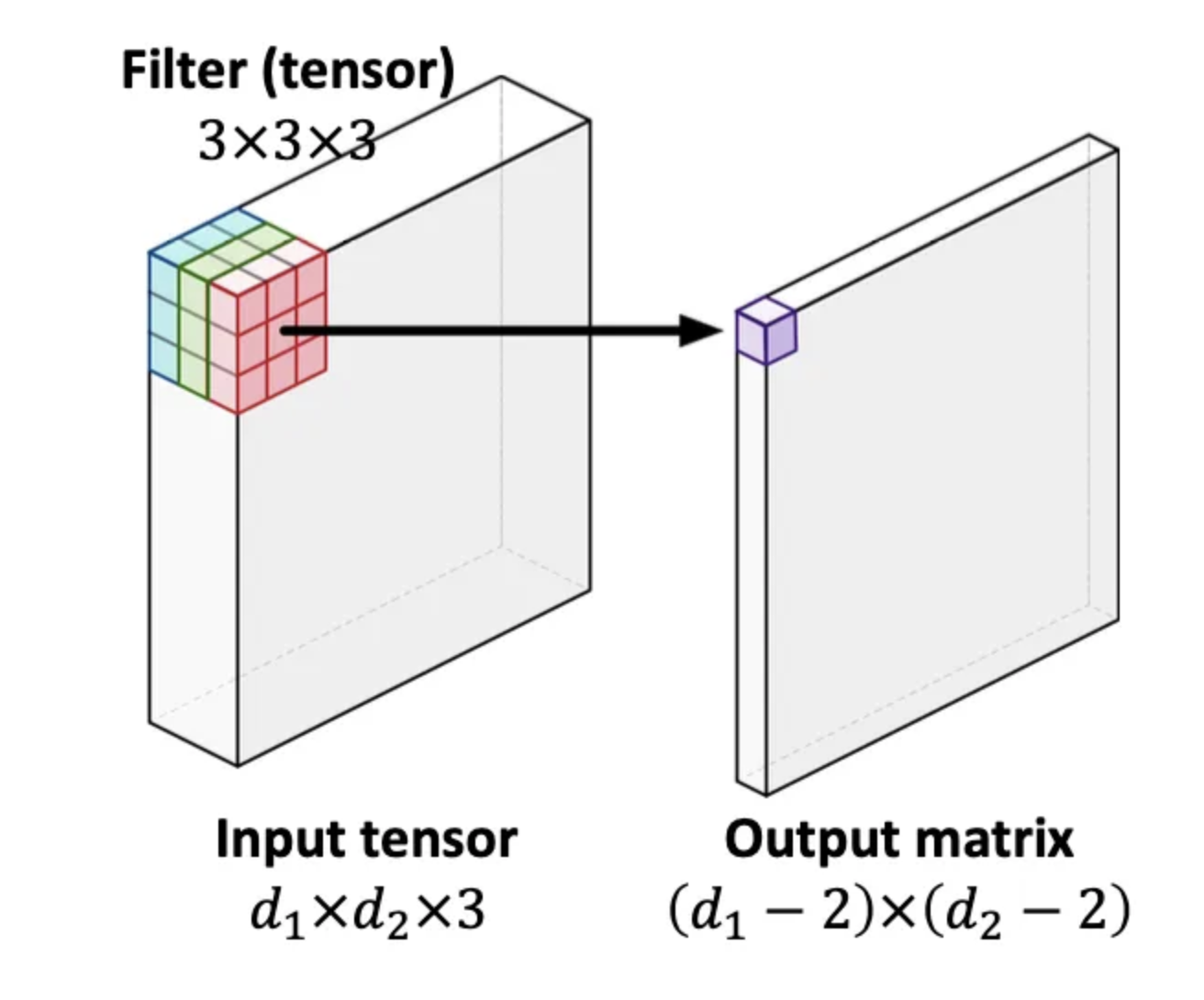
In the image provided, the filter in this particular instance will be an order-3 tensor with dimensions $k1\times k2 \times 3$. The calculation process involves using the inner product in a similar manner. Consequently, the result will indeed be in the form of a matrix.
Stride
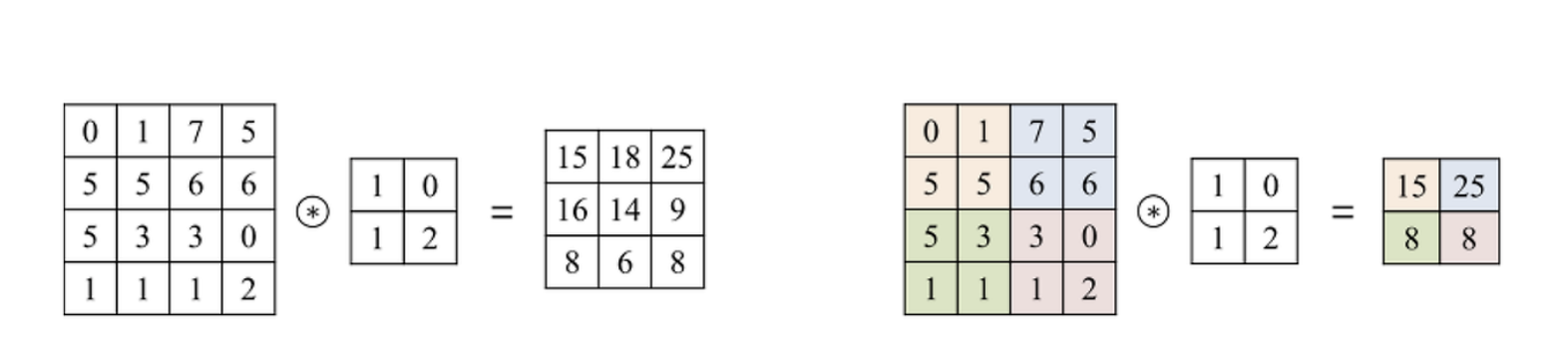
Left: Stride=1 / Right: Stride=2
When applying a filter to an image during a convolution operation, the stride is the parameter that controls how the filter moves across the image. The stride determines the amount of shift the filter makes over the image and the final size of the output image after the stride has been applied.
- Example of Stride Usage:
- Stride = 1: The filter moves one pixel at a time. This results in a more detailed feature map, capturing more information as the filter overlaps significantly with its previous position.
- Stride = 2: The filter jumps two pixels at a time. This results in a feature map that is smaller in size, effectively reducing the spatial dimensions more quickly and capturing broader features with less overlap between positions.
Padding
When we perform convolution operations, we often use padding to maintain the image's dimensions. Specifically, when we apply a smaller filter to an image, we may lose information around the edges, resulting in a smaller output feature map. To prevent this, we can add padding around the image before applying the convolution.
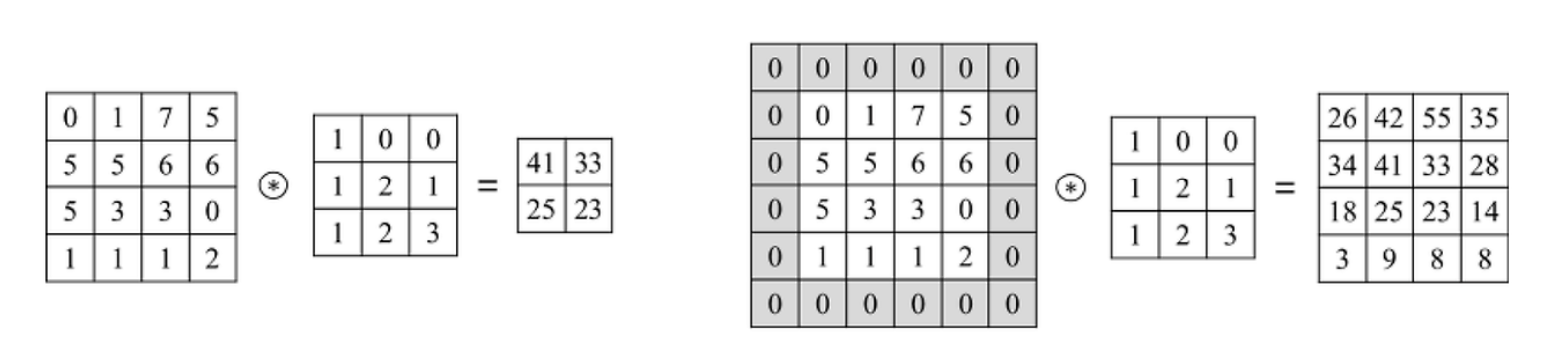
Left: Zero-padding is not applied / Right: Zero-padding is applied
Padding involves adding layers of zeros (zero-padding) around the original image dimensions. This allows the filter to be applied even at the edges of the image without reducing the size of the output. By using padding, the output feature map can maintain the same dimensions as the input image. For example, by applying one layer of zero-padding, a 4x4 image effectively becomes a 6x6 image, allowing the 4x4 filter to be applied to maintain the original image size.
Zero-padding not only helps preserve the image’s dimensions but also enables the model to learn features at the edges that would otherwise be lost or diminished.
Pooling
<img src=/images/2024-09-04-TIL24_Day67_2_DL/image-20240906193205373.png)
There exist two fundamental pooling methods: Max pooling and Average pooling. When a 2x2 pool size is applied, as illustrated in the accompanying image, the pooling operation involves selecting either the maximum value (max pooling) or the average value (average pooling) from the 2x2 matrix. This process effectively reduces the size of the result by half.
There are several types of pooling:
- Max Pooling
- Average Pooling
- Min Pooling
In images, there is a high similarity between neighboring pixels, creating patterns across the image. This similarity allows images to be represented not only at the individual pixel level but also at the level of selected areas with specific features or characteristics. The pooling layer is specifically designed to take advantage of this characteristic of image data. For example, in max-pooling, the highest value within a given area is selected to be the representative value for that area. This process helps to capture the most critical features within that area. By incorporating these pooling layers, convolutional neural networks (CNNs) are endowed with various advantageous capabilities, allowing for efficient and effective image analysis and recognition.
- Stability: Within a specific selection area, no matter how the pixels shift or rotate, the output from the pooling layer stays the same. This stability is helpful because it reduces the impact of changes like moving or rotating parts of an image on CNN's output. It keeps the network’s performance strong, even if the input images change significantly.
- Reducing size: The size of the images that CNN needs to process is significantly reduced. Thus, the number of model parameters in the artificial neural network also considerably decreases. Therefore, by using a pooling layer, the training time for CNN can be dramatically saved, and the problem of overfitting can also be alleviated.
Flatten Layer (Vectorization)
The flatten layer is a critical component that transitions the high-dimensional output of convolutional and pooling layers into a format suitable for traditional fully connected layers (also known as dense layers).
For example, after several convolution and pooling operations, an image might be represented as a 12x12x32 volume (12x12 spatial dimensions and 32 channels). The flatten layer takes this 12x12x32 volume and converts it into a single long vector of features. This results in a vector of size 4,608 (12 multiplied by 12 multiplied by 32).
Fully-Connected Layer (Dense Layer)
Now, finally, apply one or more fully connected layers and then use the softmax activation function to output the final result.
Leave a comment