Wonha Leah Shin

Specializing in AI engineering & NLP. Data Scientist by profession, decipherer of data by passion.

8 minute read

📚 The Start of Recording TIL Summer ‘24 : Why Did I Start This Project? 🚀

🔔 Don't Miss: Continous Records of TIL '25 (Still On-Going!) 🌟

✨ A New Chapter in TIL '25: Reflecting, Growing, and Moving Forward 📖

LLMs- Generating Texts, Positional Encoding, and Fine-Tuning LLMs (LoRA)



Generating Text from Large Language Models (LLMs)

  • Autoregressive LLMs
    • Autoregressive Language Models (LLMs) generate text by predicting the next token in a sequence based on the previous tokens in a sequential, step-by-step manner.
    • The model generates tokens one at a time. After predicting a token, that token becomes part of the input for predicting the next token. It continues until the end of generates [EOS] or reaches a pre-defined length.
    • $ P(w_1, w_2, \dots, w_T) = P(w_1) \cdot P(w_2 \mid w_1) \cdot P(w_3 \mid w_1, w_2) \cdot \dots \cdot P(w_T \mid w_1, w_2, \dots, w_{T-1})$
  • Greedy / Argmax Approach
    1. Token Prediction: At each step in the generation process, the model outputs a probability distribution over the entire vocabulary for the next token, based on the tokens generated so far.
    2. Argmax Selection: The model selects the token with the highest probability (i.e., the token that maximizes the probability ($P$) as the next token in the sequence. This is done by taking the argmax of the probability distribution- ($\text{argmax}_{w}P(w \vert w_1, w_2, \dots, w_t)$)
    3. Sequence Continuation: The selected token is added to the sequence, and the process repeats until an end-of-sequence token is generated or the maximum sequence length is reached.
  • Disadvantages of the Greedy/Argmax Approach
    • Lack of Diversity: Potentially leading to repetitive or overly simplistic sentences. (Maybe partially a side-effect of training with cross-entropy / softmax.)
    • Suboptimal Global Outcome: While the model is maximizing the probability of the next token at each step, it may not lead to the best overall sequence. The model can get stuck in local optima, where a high-probability word might lead to a suboptimal continuation of the sequence.
    • We have a heavy tailed output distribution.
      • Exponentially higher loss for linearly lower probability (due to the cross-entropy loss) + Exponentially lower probabilities for linear lower scores
      • It makes unlikely events far too likely to avoid high loss values.
  • Direct Sampling
    • Randomly sample the next token proportional to the probability produced by the softmax output.
  • Top-k Sampling
    • Sample from the top-k highest probability tokens at each time step
    • Use a temperature to control how “peaky” the softmax is.
    • But it can be too low-information.
      • Lots of specific choices not considered.
  • Nucleus (Top-p) sampling
    • Sample from a distribution that covers p probability mass.
    • Like top-k sampling, where k changes at each time step to cover p probability mass.

Prompts in LLMs

  • The prompt is the start of the document and then an autogressive LLMs run, then add its own text.
  • LLMs are highly sensitive to the prompt.

  • How do we construct the right prompt to elicit the behavior we want?

  • Prompt Engineering
    • The process of designing the input that is used to prompt a machine learning model in order to produce the desired outputs from the model.
    • In-Context Prompting
      • For pre-trained models, often involves a lot of hacking to figure out the prompt to get the desired output.
  • Types of Prompt Engineering
    • Zero-shot learning: feeds the task into the model and ask for the results.
    • Few-shot learning: gives the LLM multiple examples.
    • Expert-Prompting: Augment the instructions by telling the system to be an expert and giving it an identity, e.g., a famous scientist.
    • Chain-of-Thought(CoT) Prompting: generates a sequence of short sentences to describe reasoning logic step-by-step. It can help complicated reasoning tasks.
      • CoT for few-shot: adds in the line “give detailed explanations for the answer.”
      • CoT for zero-shot: adds in the line “Let’s think step by step.”: will produce much longer outputs.
      • CoT is much more effective for large LLMs.

  • Position Encoding

    Positional encodings are a technique used in Transformer models to provide information about the position or order of tokens in a sequence. This is important because Transformers do not have a built-in mechanism to understand the order of tokens, unlike models such as Recurrent Neural Networks (RNNs), which inherently process data sequentially.

    • By default, transformers are permutation invariant, i.e., they don’t care about the order of the tokens.
    • In Transformers, all tokens are processed in parallel (thanks to self-attention), so without positional information, the model would treat each token as if they were independent of one another, disregarding their order. Positional encodings solve this issue by adding information about the position of each token to its embedding, enabling the model to capture the relative or absolute positions of tokens in the input sequence.
    • How Positional Encodings Work:
      • Input Embeddings: Each token in a sequence (e.g., words or subwords) is first mapped to a dense vector (embedding) through the embedding layer. These embeddings represent the semantic meaning of the tokens.
      • Adding Positional Information: To incorporate positional information, positional encodings are added (or concatenated) to the token embeddings. These positional encodings provide the model with information about the position of each token in the sequence. The positional encodings are vectors of the same dimension as the token embeddings, and each position in the sequence gets a unique positional encoding.
      • Combination: The final input to the Transformer model is the sum of the token embeddings and their corresponding positional encodings. This allows the model to take both the content of the tokens and their order into account when applying attention mechanisms.

    • Formula:
      • $PE(pos, 2i) = \sin\left(\frac{pos}{10000^{2i/d}}\right)$, $PE(pos, 2i+1) = \cos\left(\frac{pos}{10000^{2i/d}}\right)$
      • The reason for using both sine and cosine functions is to allow the model to capture the relative positions between tokens. For example, the difference in the encodings of two tokens can be directly derived based on their positions.
    • For position embeddings, we specify the maximum context length and the dimensionality of the embedding.


  • Types of Position Embeddings
    • Absolute Position Embeddings: used in the original transformer. It constructs a d-dimensional vector, where one line gives values for the even rows and one line for odd rows. It assigns a unique positional encoding to each token based on its absolute position in the sequence.
      • This method represents the actual position of each token in the input sequence relative to the start of the sequence, using a predefined or learned positional encoding vector. If we use sinusoidal positional encodings, the position encoding would be deterministic.
      • Disadvantages- No Flexibility for Sequence Length: If the input length exceeds the maximum sequence length for which the positional encodings were trained, the model may struggle. Additionally, longer sequences in test data may not generalize well.
      • Lack of Relative Positional Awareness: The model only knows the absolute position of each token, not how tokens relate to one another (e.g., it cannot natively reason that one token is two positions ahead of another).
    • Relative Position Embeddings: Relative position embeddings encode the relative distances between tokens, rather than their absolute positions in the sequence. Relative position information is encoded in the values and keys by modifying self-attention.
      • The attention mechanism is modified to incorporate the relative distance between tokens.
      • For the sentence “The cat sat on the mat.”, instead of embedding token positions 1, 2, 3, etc., the model would embed the relative distances between tokens. For example: “cat” might be 1 position away from “The”. “on” might be 2 positions away from “cat”.


  • Rotary Positional Embeddings (RoPE)

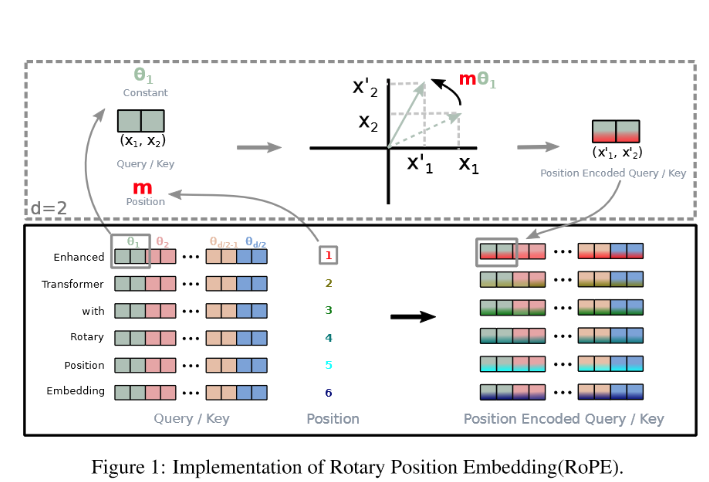
    • RoPE (Rotary Positional Embedding) is a method of encoding positional information in Transformer models, specifically designed to improve the way self-attention mechanisms handle positional information. Unlike traditional absolute or relative positional encodings, RoPE allows Transformers to better generalize to longer sequences and capture relative position information without explicitly modifying the architecture of the attention mechanism.

    • Today, this is the method most widely adopted. Used by LLaMA, Phi-1.5, and others.



    • Rotational Invariance: RoPE uses a rotary transformation of the query and key vectors in the self-attention mechanism.

    • Compatibility with Self-Attention: Instead of adding positional encodings directly to the input embeddings (like absolute positional encodings), RoPE applies a rotation to the query and key vectors based on the token’s position.

    • Longer Sequence Generalization: RoPE allows better generalization to longer sequences by leveraging the properties of rotary transformations, which maintain information about token positions regardless of sequence length.

    • Rotation Matrix

      • Given a token’s position $pos$, the RoPE method modifies the query $Q$ and key $K$ vectors by rotating them using a rotation matrix dependent on the token’s position.
      • This rotary transformation ensures that tokens’ relative positions are encoded during the attention computation in a continuous and smooth manner.


Fine-Tuning LLMs

  • Fine-Tuning the Entire LLM is Very Expensive

    • Updating the entire network requires roughly 3x the memory of the forward pass. The backward pass requires storing data from the forward pass and computing new data re-used for the backward pass.

  • LoRA (Low-Rank Adaptation)

    LoRA (Low-Rank Adaptation of Large Language Models) is a technique used to fine-tune large pre-trained language models efficiently by introducing low-rank updates to the model’s parameters.

    • Not all of parameters need to be fully updated during the fine-tuning process for every new task. Instead, LoRA proposes the idea that the update to the parameters can be represented in a low-rank matrix form. LoRA introduces learnable low-rank matrices that are used to adjust only a subset of the parameters.
    • Modify chosen weight matrices to include two new matrices: $h = W_0x + \Delta W_x = W_0 x + B A_x$
    • W is from the original pre-training, and we only update B and A. The inner dimension (rank) is small so that BA has the same dimensions of W, but there are far fewer parameters that can change.
      • $W$ is the original weight matrix.
      • $\Delta W = BA$ represents the low-rank update.
      • $A \in \textbf{R}^{d \times r}$ and $B \in \textbf{R}^{r \times d}$ are learnable low-rank matrices.
      • $r$ is the rank, which is the smaller than the original dimeionsion $d$, making $\Delta W$ much smaller than $W$.
      • $BA$ initialized to be a 0 matrix.
      • $A$ initialized randomly from a Gaussian distribution.
      • $B$ initialized to be a 0 matrix.
      • One must tune the rank r of $BA$.
    • LoRA can be used effectively in other pre-trained architectures as well, e.g., diffusion models, ConvNextv2, etc.
    • After fine-tuning with LoRA, can fold the weights into the original to reduce compute after fine-tuning.
    • Disadvantage: It requires expensive activation memory consumption in the LoRA layers because the large input activation needs to be stored for the feed-forward pass.



Leave a comment

You may also enjoy