Day99 Deep Learning Lecture Review - Lecture 16

📚 The Start of Recording TIL Summer ‘24 : Why Did I Start This Project? 🚀

🔔 Don't Miss: Continous Records of TIL '25 (Still On-Going!) 🌟

✨ A New Chapter in TIL '25: Reflecting, Growing, and Moving Forward 📖

Uncertainty in Deep Learning, Distribution Shifts, Model Calibration, and Out-of-Distribution (OOD) Detection

1. Types of Uncertainty

• Aleatoric Uncertainty (stochastic uncertainty)
  • Caused by random noise inherent in data or experiments.
  • Present in observations and needs to improve with more data.
  • Where model predictions have high error.
• Epistemic Uncertainty
  • Due to the need for more knowledge or training data.
  • This can decrease as the model encounters more diverse data.
  • Where we lack of data to feed through the model.
• Both forms of uncertainty are present in most deep-learning models.
• Users will use a system on data that may differ from the training data.
  • We have epistemic uncertainty in areas where we lack data
• We want models to be:
  • Robust to distribution shift.
  • Aware of when it happens using uncertainty estimation methods.
• Types of Uncertainty in Deep Learning
  • Robustness to distribution shift
  • Classifier threshold selection
  • Model calibration
  • Detecting out-of-distribution inputs
  • Conformal prediction - an uncertainty-aware framework
    
    

2. Robustness to Distribution Shift

• Making Models Robust to Distribution Shift

  • There are many different methods, but most need to work better.
  • Successful approaches in vision:
    • (Extreme) data augmentation
    • Conditional generative models take input from a source distribution and modify it to resemble the target distribution.
    • We need a lot of data for this.

• Training & Evaluation Strategy

  • We often have abundant data from distribution A, but very little from distributions B, C, D, and others.
  • How can we determine if modifications in the model or training process (augmentations) enhanced the system's robustness to distribution shifts?
  • General Recommendations
    • Do not train on A mixed with minority data B. This will improve the performance on B, but we won’t know for the others!
    • Reserve minority data for performance evaluation and picking an operating threshold for the model.
    • Operating threshold: The prediction score exceeds the threshold to establish the category.
  • Example
    • A significant distribution shift will occur if all training data comes from a single hospital.

• Picking a Threshold

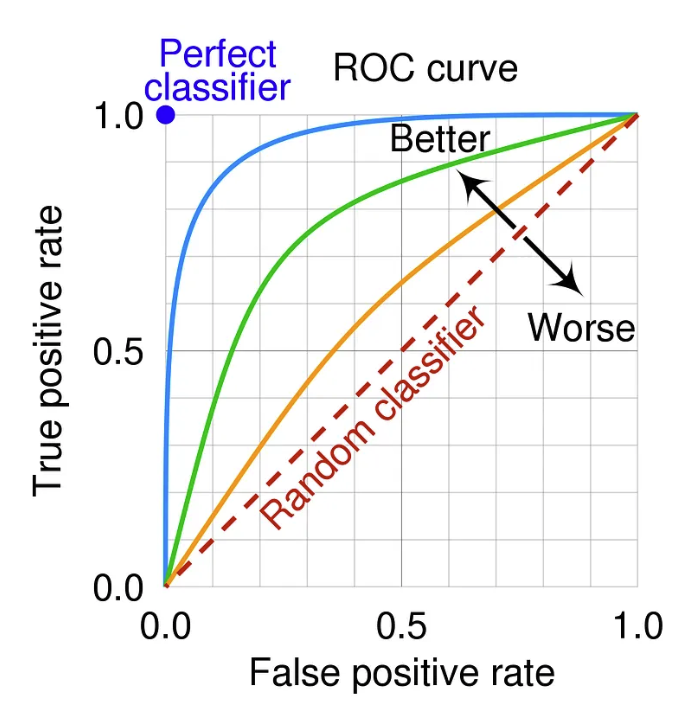
  • Most cases require more than AUC and probability scores for production systems.

    • We need to choose an operating threshold.
    • We want to choose a threshold that is robust across all distributions.

  • AUC is the area under the curve, so we don’t have to choose a threshold.

    • But this is not a universal threshold.
      
      

    Image Source: Medium- ROC Curve and AUC: Evaluating Model Performance by ilyurek K

    
    
    

  • Sweep a threshold across all evaluation sets from different distributions to compute an evaluation metric, such as accuracy or F1-score.

  • Choose the threshold that achieves desirable performance across all distributions.

• Operating Threshold

  • We need a universal threshold that works best for all distributions.
    • May only draw curve if minimum criteria are met,
      • e.g., sufficiently high recall and low false positive rate for product needs.
    • Average across all curves and choose threshold corresponding to the maximum point.
      
      
      

3. Model Calibration

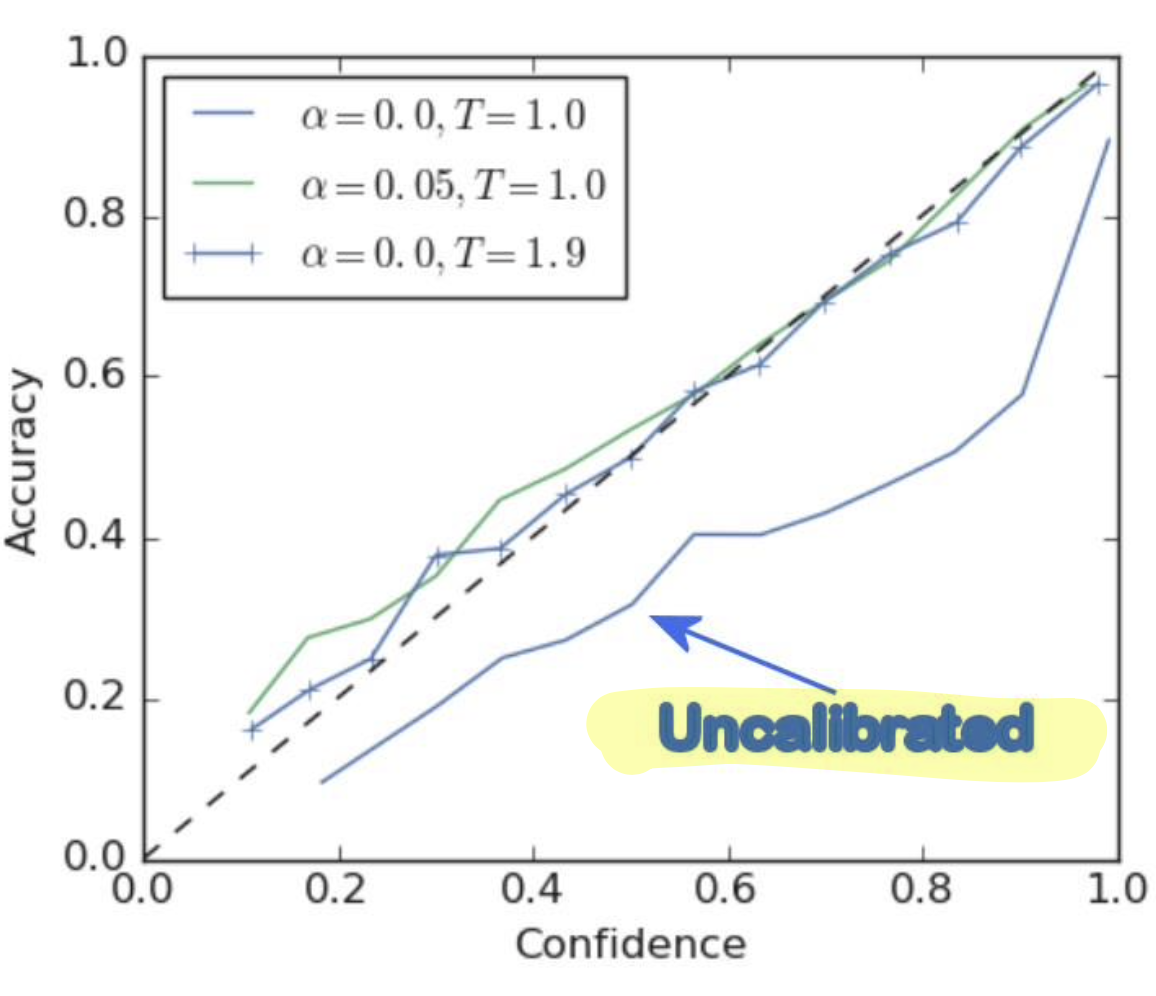
If a model is calibrated, then the estimated class probabilities are consistent with what should naturally occur. So, if a logistic regression classifier iss calibrated then a score of 0.7 would mean it is the positive class 70% of the time. For binary classification, we can use a model calibration plot to inspect.

• Most Networks are poorly calibrated
  • Good Calibration: If a sample has a sftmax score of 0.8 then it says it has an 80% chance of being the target class
  • In practice, these “probabilities” are not well calibrated when we train our networks
    • Interpreting the output of a softmax as a set of probabilities is not a good idea unless you know the model is calibrated.

1. Platt Scaling

In machine learning, Platt scaling or Platt calibration is a way of transforming the outputs of a classification model into a probability distribution over classes.

• Key Essentials:

  • Model calibration for binary prediction
  • Done in a post-hoc manner.
  • Train a binary classifier first that outputs a score, e.g., a non-calibrated probability.
  • Platt Scaling requires a calibration set.
  
  
  

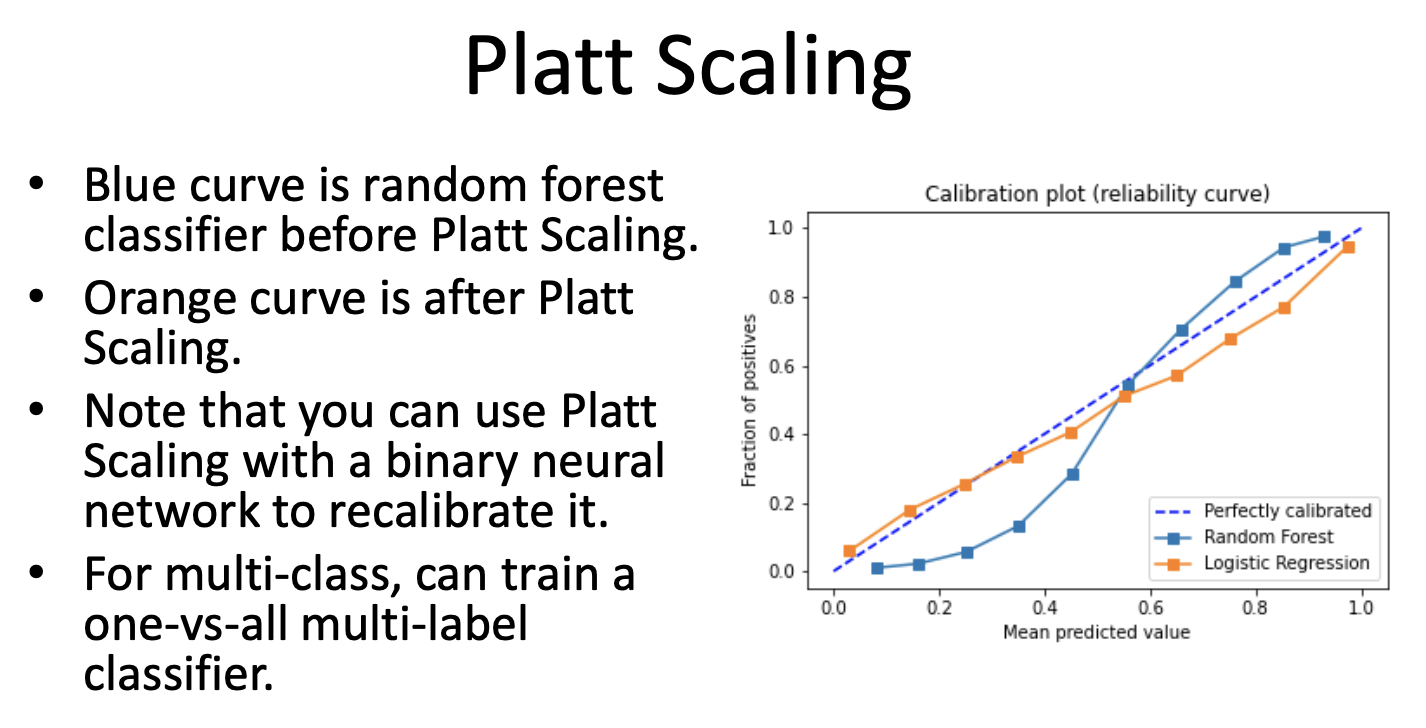
Explanation Source: Wikipedia: Platt Scaling

• Platt scaling is an algorithm to solve the aforementioned problem. It produces probability estimates.

  $P(y=1 \vert x) = \frac{1}{1+\text{exp}(A(f(x))+B)}$
  
  $t_+ = \frac{N_+ + 1}{N_{-}+2}$ for positive samples ($y=1$), and
  $t_- = \frac{1}{N_{-}+2}$ for negative samples ($y=-1$)
  • Using trained model, run it on the calibration set not used for training to get the $f(x)$ values.
  • Learn two scalars ($A$ and $B$) by fitting a univariate logistic regression model to these scores, where targets are probabilities (rather than 1 or 0).
  • The parameters $A$ and $B$ are estimated using a maximum likelihood method that optimizes on the same training set as that for the original classifier $f$.
  • To avoid overfitting to this set, a heldout calibration set or cross-validation can be used.
  • This transformation follows by applying Bayes’ rule to a model of out-of-sample data that has a uniform prior over the labels.
  • The constants 1 and 2, on the numerator and denominator respectively, are derived from the application of Laplace smoothing.

• Platt scaling has been shown to be effective for SVMs as well as other types of classification models, including boosted models and even naive Bayes classifiers, which produce distorted probability distributions

• It is particulary effective for max-margin methods such as SVMs and boosted trees, which show sigmoidal distortions in their predicted probabilities, but has less of an effect with well-calibrated models such as logistic regression, multilayer perceptrons, and random forests.
  
  

2. Label Smoothing and Soft-Targets

Label smoothing is a regularization method used on the output labels of classification models. Rather than relying on strict labels (0s and 1s) as targets, label smoothing adjusts these labels to introduce some ambiguity by allocating a portion of the probability mass to incorrect classes. This strategy encourages the model to have less certainty in its predictions, thereby enhancing its performance on unseen data.

• Training with One-Hot Targets is One Cause for Models Being very Poorly Calibrated AFter Training
  • We do not actually need to use one-hot targets with softmax.
  • All softmax requires is a target vector that sums to 1.
    
    

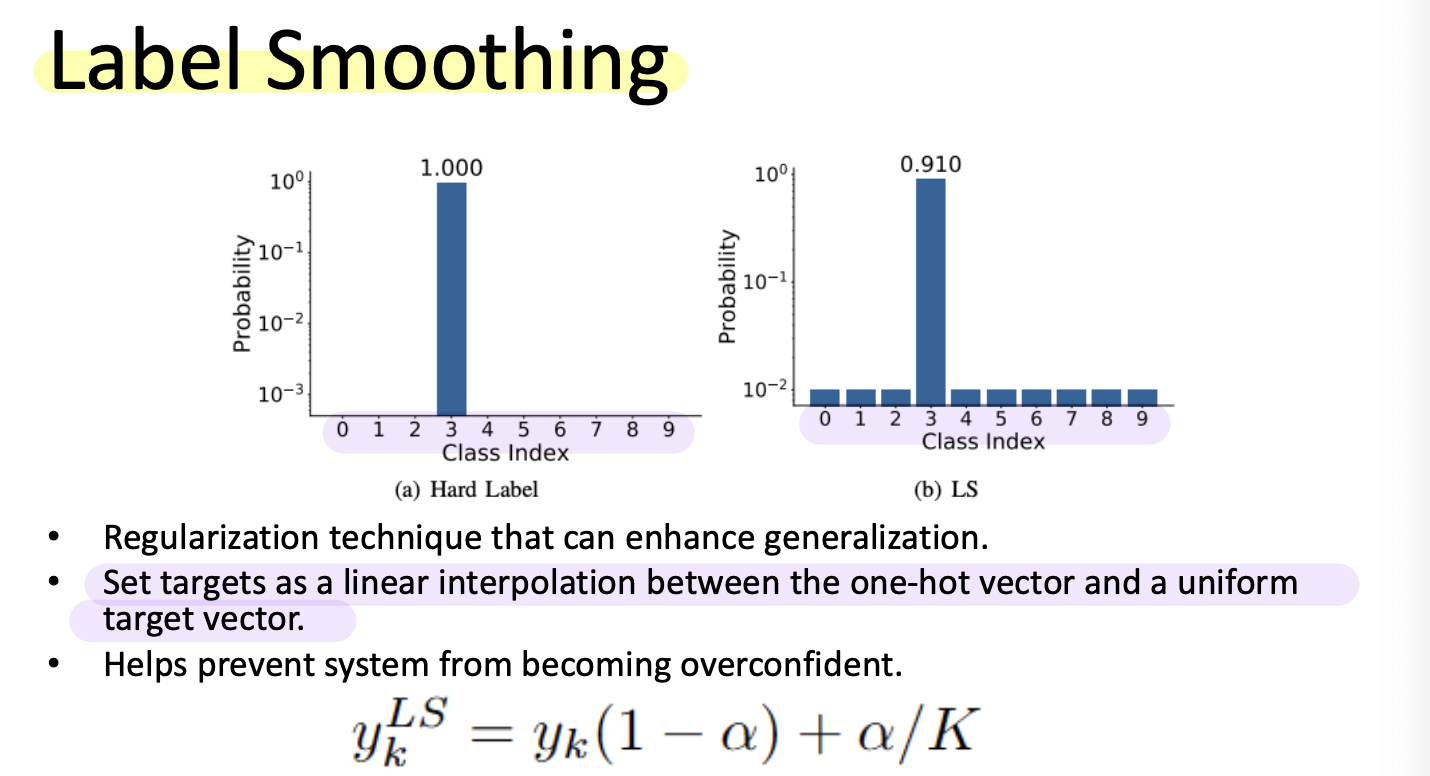
where $K$ is the number of label classes, and $\alpha$ is a hyperparameter that deermines the amount of smoothing.

If $\alpha = 0$, we obtain the original one-hot encoded $y_k$. If $\alpha=1$, we get the uniform distribution.

• Label Smoothing is Built Into PyTorch

  torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100,
                           reduce=None, reduction='mean', label_smoothing=0.0)
  

• Label Smoothing helps calibration

• Label smoothing gives better calibration without post-hoc temperature scaling.

  Image Source: Delving Deep into Label Smoothing, Chang-Bin Zhang et el.
  
  
  

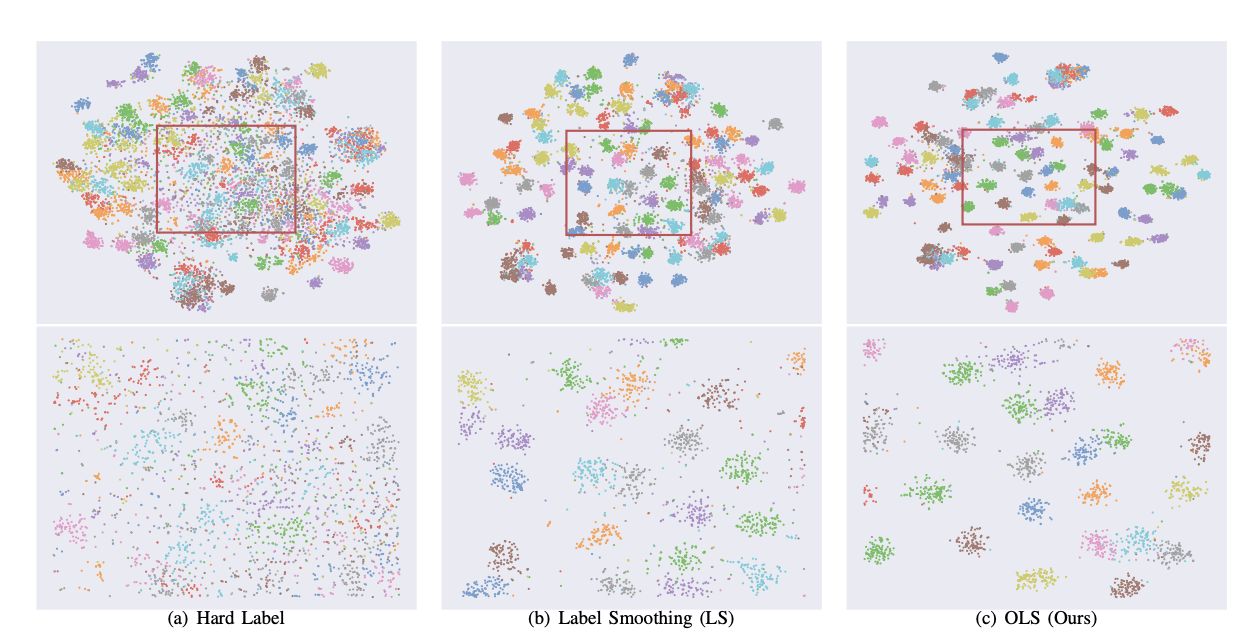
  After implementing label smoothing, we could observe that the clusters are clearly distinguished.
  
  

4. Detecting Out-of-Distribution Inputs

Out-of-Distribution (OOD) detection is the capability of a model to identify and appropriately manage data that significantly differs from its training set.

• We must identify when epistemic uncertainty is elevated to effectively reject out-of-distribution inputs.
  • Simply using a threshold will not suffice.
• Various papers refer to this concept using different terms:
  • Selective Classification
  • Out-of-Distribution Detection
  • Open-Set Recognition
• Closed-World vs. Open-World
  • Closed-World: Assumes all test inputs come from classes seen during training.
  • Open-World: Assumes test inputs may come from classes not seen during training and must be identified.
    
    
• Selective Classification: Assumes that all inputs belong to classes the model was trained to recognize, yet some inputs may significantly differ from the training data.
  • Train a classifier to distinguish between roses and non-roses, but only train on red roses for the positive class.
  • If a white rose is inputted, it will be rejected.
• Out-of-Distribution Detection (OOD): Assumes OOD samples are from a very different distribution.
  • Model is trained on MNIST but then must reject images from ImageNet
• Open Set Recognition: It presumes that out-of-distribution (OOD) samples originate from a distribution simliar to the training data, although some classes were not encountered during training.
• The Same Problem
  • Algorithms designed for these issues can theoretically address the others as well.
  • Communities tend to be insular, and often papers focus on testing only one of these setups; however, all of them can theoretically be applied to the general problem.
  • Generally speaking, out-of-distribution (OOD) detection (MNIST vs. ImageNet) is significantly easier than open set recognition (ImageNet-1K vs ImageNet-21K).
    
    

Identifying Out-of-Distribution (OOD) Inputs: Methods

• Threshold Based Methods for Binary

  • If models are well calibrated, unknown inputs are likely to be near the threshold.
  • Choose two thresholds instead of one operating threshold
    • We need OOD samples to tune this.

• General Formulation

  $\hat{y} = \begin{cases} \text{argmax}_k F(X) \space\space\space \text{if} \space S(X) \geq \delta \\ K+1 \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space \space \text{if} \space S(X) < \delta \ \space \end{cases}$
  • Assign the most likely class from $F(X)$ if the acceptance score $S(X)$ is above a threshold.
  • Otherwise, classify the input as the unkonwn $(K+1)$ class.
  • Ideally, $S(X)$ scores for in-distribution and out-of-disribution inputs do not overlap for choosing a threshold

• Tuning the Threshold

  • Tuning the threshold is challenging

• Two Complementary Thrusts

  • Methods for learning features that facilitate identifying OOD inputs
    • Using regularization, different losses, augmentation strategies, etc.
  • Methods for identifying OOD inputs
    • Algorithms for computing $S(X)$

Identifying Out-of-Distribution (OOD) Inputs: Computing $S(X)$

• Confidence Thresholding ($\tau$-Softmax)
  • Compute the most likely class bycomputing the argmax of the softmax classification score.
  • If the score is below a given threshold then the input is considered OOD
  • Ideally, the softmax is a uniform distribution for OOD inputs, but models are not calibrated to permit it.
• ODIN
  • Confidence thresholding wiht temparature scaling on the softmax and applying a small input perturbation based on the gradient of the temperature adjusted softmax.